Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 36
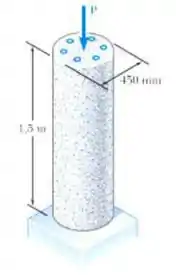
Para a coluna do Problema 2.35, determine a força centrada máxima que pode ser aplicada se a tensão normal admissível é de 20 ksi no aço e 2,4 ksi no concreto.
Passo 1
Fala aí galera tudo belezinha? Antes de determinarmos P vamos calcular a deformação de ambos os materiais, aço e concreto, vem comigo :D
Aço:
Concreto:
Notem que o valor que “governa” é a menor deformação que no caso é a do concreto
Passo 2
Vamos determinar a área da coluna, vem comigo !!
Substituindo na equação temos:
Para determinarmos a forca P é necessário realizar a soma P do aço e do concreto como se segue abaixo
Resposta
Exercícios de Livros Relacionados
Uma barra maciça de latão de 150m m de comprimento e 10m m de diâmetro se ajusta perfeitamente, dentro de um tubo de mesmo comprimento, com 15m m de diâmetro externo e 10m m de diâmetro interno. Uma p
Duas barras cilíndricas maciças A C e C D , ambas de mesma liga de alumínio ( E = 70G P a ) , são soldadas juntas em C e submetidas ao carregamento indicado. Determinar ( a ) a deformação total da bar
Para a barra composta do Prob. 2.10, determinar: ( a ) a carga P , para que a deformação total da barra seja - 0,2m m ; ( b ) a correspondente deflexão do ponto B .
Determinar a deformação da barra composta do Problema 2.34, se nela atuar uma força centrada de intensidade P = 45 k N .
Uma barra de 250 m m de comprimento, com seção transversal retangular de 15 × 30 m m , consiste de duas lâminas de alumínio ( E = 70 G P a ) , de 5 m m de espessura, e no centro de uma lâmina de latão