Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 34
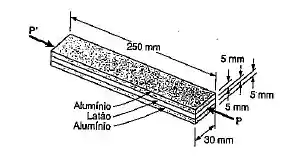
Uma barra de de comprimento, com seção transversal retangular de consiste de duas lâminas de alumínio (, de de espessura, e no centro de uma lâmina de latão com a mesma espessura. Se ela está sujeita a uma força centrada, determinar a tensão normal (a) nas lâminas de alumínio; (b) na lâmina de latão.
Passo 1
Fala aí galera, bora ficar craque em Resmat com mais essa questão.
Vamos considerar , como cargas compartilhadas por hastes de alumínio e latão, respectivamente.
Vamos equacionar a soma das cargas compartilhadas pelas hastes de aluminío e latão com a força aplicada na barra.
Vamos escrever as deformações induzidas em membros de alumínio e latão como segue:
Passo 2
Onde, os membros de alumínio e latão se deformam em quantidades iguais e, portanto,
Substituindo
Como
Passo 3
Agora iremos substituir a equação (2) na equação (1)
Passo 4
Vamos calcular a razão de
Vamos calcular a espessura das camadas de alumínio
Vamos substituir os valores numéricos
Passo 5
Vamos substituir os valores numéricos na expressão(3)
Vamos substituir o valor de em .
Passo 6
Vamos calcular a magnitude da carga usando a seguinte expressão:
Passo 7
Vamos calcular a área da seção transversal das camadas de alumínio e latão da seguinte maneira:
- Vamos calcular a tensão nas camadas de alumínio usando a seguinte expressão
Substituindo
Portanto, a tensão normal nas camadas de aluminío é de
Passo 8
- Vamos calcular a tensão nas camadas de latão usando a seguinte expressão
Substituindo
Portanto, a tensão normal nas camadas de latão é de
Resposta
- Portanto, a tensão normal nas camadas de aluminío é de
- Portanto, a tensão normal nas camadas de latão é de