Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 58

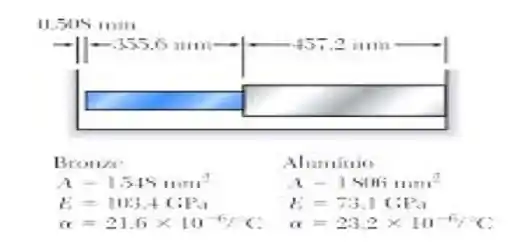
Sabendo que existe um espaçamento de 0,508 mm quando a temperatura é de 23,9°C, determine (a) a temperatura na qual a tensão normal na barra de alumínio será igual a -75,8 MPa e (b) o comprimento exato correspondente da barra de alumínio.

Passo 1

Fala aí galerinha tudo belezinha? Para determinarmos a temperatura na qual tensão normal na barra de alumínio será igual a -75,8 Mpa, vamos primeiramente determinar encurtamento, vejam o esboço abaixo :D

σ α = - 75,8   M P a   = - 75 × 10 6   P a

P = -   σ α A α = - 75 ×   10 6 ×   18 06 × 10 - 6 = - 135.45   k N

Encurtamento devido a carga P é dada por:

δ ρ = P L b E b   A b   + P L a E a A a  

= 135.45 × 10 3 ×   0.3556 103,4 ×   10 9     × 1 548 × 10 - 6 +   135.45 × 10 3 ×   0,4 572 73.1 × 10 9 1806 × 10 - 6

δ ρ = 0,000300919 + 0.000469083

δ ρ = 0.000770002   m m

δ ρ = 770.002 × 10 - 6 m

E o alongamento devido expansão térmica é dado como:

δ t = 0 , 000508 + 770.002 × 10 6

= 0.001278 = 1,278 × 10 - 3 m

Passo 2

Se considerarmos :

δ T = L b   ∝ b ∆ T +   L a α a ∆ T

= 0.3556 21.6 × 10 - 6 ∆ T + 0.4572 23.2 × 10 - 6 ∆ T

δ T = 18.288 × 10 - 6 ( ∆ T )

Igualando temos:

18.2 88   x   10 - 6     ∆ T = 1,278 × 10 - 3  

    ∆ T = 69.88 ° C

a    

∆ T q u e n t e = T f r i o + ∆ T

∆ T q u e n t e = 23,9 + 69.88

∆ T q u e n t e = 93,78   ° C

b

δ a =   L a α a     ×     ∆ T -   P L a E a   A a

= 0.4572 ×   23,2 ×   10 - 6   ×   69.88 - 135.45 × 10 3 ×   0.4572 73,1   x   10 9   × 1 806 × 10 - 6

= 0.000272137 = 0,272137 × 10 - 3 m L b = 0.4572 + 0,272137 ×   10 - 3

L b = 0.457472137   m

Resposta

  1. 93.78   ° C
  2. ≅ 0.457 5   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considerando que a viga prismática AB tem uma seção transversal retangular, mostre que para a carregamento indicado o valor máximo da densidade de energia de deformação na viga é M m a z = 45 8 U V Em
Na montagem mostrada, os torques T AeT B são aplicados nos discos A e B, respectivamente. Sabendo que ambos os eixos são maciços e feitos de alumínio ( G = 73G P a ) , determine a energia de deformaçã
Mostre por integração que a energia de deformação na barra cônica AB é U = 7 48 T 2 L G J m i n em que J m i n é o momento polar de inércia na barra na extremidade B.
A s especificações de projeto para o eixo de aço AB exigem que o eixo absorva uma energia de deformação de 400i n ∙ l b enquanto se aplica um torque de 25 k i p ∙ i n . Utilizando G = 11,2 × 10 6 p s
σ E = 160 M P a . Usando o critério da máxima energia de distorção , determine o intervalo de valores de σ z para o qual não ocorre o escoamento.