Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 13
Duas barras cilíndricas maciças e , ambas de mesma liga de alumínio , são soldadas juntas em e submetidas ao carregamento indicado. Determinar a deformação total da barra composta ; a deflexão do ponto .
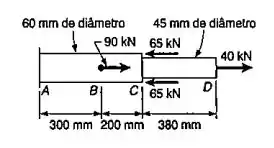
Passo 1
Fala aí galera, bora fazer mais uma questão de Resmat. Primeiramente, vamos encontrar a áreas das seções e . Para , temos:
Já para a seção , temos:
Temos que
Com isso, podemos encontrar a deformação total da barra, dada por:
Substituindo, temos que:
Passo 2
Para determinarmos a deflexão, temos que ela é dada por:
Resposta
Exercícios de Livros Relacionados
Um tubo de latão de 300m m de comprimento, com 30m m de diâmetro externo e 3m m de espessura, é fixado em um torno mecânico manual, que está ajustado de tal modo que os mordentes encostem nas suas ext
Uma coluna de concreto de 1,2m é reforçada por quatro barras de aço, cada uma de 20m m de diâmetro, como indicado. Sabendo-se que para o aço E = 200G P a e α = 11,7 × 10 - 6 / ° C e para o concreto E
Um trilho de aço ( E = G P a ; α = 11,7 × 10 - 6 / ° C ) de estrada de ferro foi estendido a uma temperatura de - 2 ° C . Determinar a tensão normal no trilho quando a temperatura atingir 50 ° C , con
A montagem mostrada consiste em um tubo de alumínio ( E = 70G P a ; α = 23,6 × 10 - 6 / ° C ) preenchido com núcleo de latão ( E = 105G P a ; α = 20,9 × 10 - 6 / ° C ) e, com ausência de tensão a uma
A montagem mostrada consiste em um tubo de alumínio ( E = 70G P a ; α = 23,6 × 10 - 6 / ° C ) preenchido com núcleo de aço ( E = 20 0G P a ; α = 11,7 × 10 - 6 / ° C ) e, com ausência de tensão a uma t