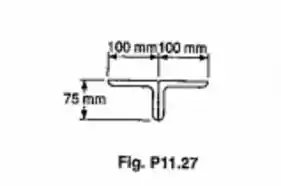
Um membro em compressão, de comprimento efetivo igual a 3,6m, é feito soldando-se juntos dois perfis laminados de aço L100X75X6,35mm, como mostrado. Usando-se E=200GPa, determinar a carga centrada admissível para o membro, se um coeficiente de segurança de 2,5 é desejado.
Passo 1
Fala aí, bora fazer esse exercício de peso admissível.
Beleza, até aqui a gente calculou bastante peso crítico que era dado por:
O peso admissível é parecido, é uma parcela do peso crítico que é aceitável para um determinado fator de segurança e pode ser calculado assim:
Maneiro, temos quase tudo nessa brincadeira, vamos ter que correr atrás do momento de inércia da seção.
Passo 2
Já te digo de cara que não vá perdendo seu tempo calculando esse tipo de momento de inércia á mão, esses perfis possuem um raio interno característico dos perfis L que não podem ser bem aproximados por retângulos. Sendo assim vamos caçar nas tabelas do fim do livro o valor do momento de inércia para o perfil mostrado.
O equivalente ao perfil apresentado é o perfil L102x76x6,4mm retirado da tabela do apêndice C para cantoneiras de abas desiguais.
Temos:
E:
Em relação as tabelas esse tipo de peça se encontra numa posição trocada.
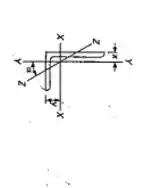
sendo assim aqui teremos de calcular os momentos de inércia para as duas direções, que como foram trocadas serão dados por:
E
Onde:
é a área da seção:
é a distância entre os eixos, central do sistema e de cada peça que são simétricas.
Ambos os valores são retirados da mesma tabela:
E a distância dos eixos vai ser no eixo x, porém na tabela a maior aba está na vertical então retiramos o valor de y das tabelas que para nós ficará em x.
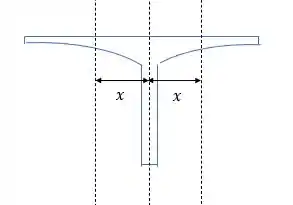
Voltando a equação do momento de inércia substituindo os valores temos:
E aí:
E:
Acaba sendo o eixo fraco.
Passo 3
Daqui, podemos voltar ao peso crítico:
Substituindo os valores, temos:
E para o peso admissível com o fator de segurança de 2,5: