Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 55

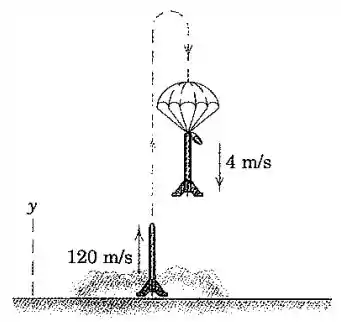
O combustível de um modelo de foguete é queimado tão rapidamente que se pode assumir que o foguete adquire a sua velocidade de queima total de 120   m / s enquanto continua essencialmente no nível do solo. O foguete então continua sem propulsão verticalmente para cima até o ápice da trajetória. Com a inclusão do arrasto aerodinâmico, a aceleração na direção y durante este movimento é a y = - g - 0,0005 v 2 , onde as unidades são metros e segundos. No ápice um paraquedas se abre do cone do nariz, e o foguete rapidamente adquire uma velocidade de descida constante de 4   m / s . Estime o tempo de voo t .

Passo 1

Galera, vamos primeiro tentar achar tempo t s do solo até o ápice. Como temos a expressão da aceleração a y = - g - 0,0005 v 2 em termos da velocidade, temos que usar uma equação diferencial que relacione essas três coisas: velocidade, aceleração e tempo.

Então, podemos usar a seguinte equação diferencial:

a   d t = d v

Substituindo o valor de a y :

- g - 0,0005 v 2   d t = d v

Passo 2

Show! Agora, vamos dar uma ajeitadinha na equação e integrá-la:

d t = - 1 g + 0,0005 v 2   d v

Lembre-se que o foguete parte do solo com 12 0   m / s e alcança o ápice com velocidade nula:

∫ 0 t s d t = - ∫ 12 0 0 1 g + 0,0005 v 2   d v

Consultando uma tabela de integrais, vemos que:

t 0 t s = - 1 0,0005 g a r c t g 0,0005 g v 120 0

t s - 0 = - 1 0,0005 g a r c t g   0 - a r c t g 120 0,0005 g

t s = 1 0,0005 g a r c t g 120 0,0005 g

Substituindo g = 9,8   m / s 2 , temos:

t s = 10,1   s

Passo 3

Beleza! Para encontrar o tempo de descida t d , como a velocidade passa a ser constante, só precisamos saber qual é a altura máxima atingida pelo foguete. E isso podemos calcular usando a seguinte equação diferencial:

a   d s = v   d v

Substituindo o valor de a y (durante a subida):

- g - 0,0005 v 2   d s = v   d v

d s = - v g + 0,0005 v 2   d v

Agora vamos integrar:

∫ 0 h d s = - ∫ 120 0 v g + 0,0005 v 2   d v

s 0 h = - 1 2   .   0,0005 ln ⁡ g + 0,0005 v 2 120 0

h - 0 = - 1 0,001 ln ⁡ g - ln ⁡ g + 0,0005 120 2

h = - 1 0,001 ln ⁡ g g + 7,2

Fazendo-se g = 9,8   m / s 2 , obtemos a altura máxima:

h = 550,8   m

Passo 4

Galera, como a velocidade é constante na descida, o tempo é dado por:

t d = h v = 550,8   m 4   m / s = 137,7   s

Então, o tempo total vai ser:

t = t s + t d = 10,1 + 137,7 = 147,8   s

Resposta

t = 147,8   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o raio de curvatura da trajetória descrita pela partícula do Problema 11.96 quando t = 0, A = 3 e B = 1.
A trajetória de uma partícula P e um caracol de Pascal. O movimento da partícula e definido pelas relações r = b(2 + cos θ ) e θ = π t, onde t e θ são expressos em segundos e radianos, respectivamente
O movimento bidimensional de uma partícula e definido pelas relações r = 2b cos ω t e θ = ω t, onde b e ω são constantes. Determine (a) a velocidade e a aceleração da partícula em qualquer instante, (
A oscilação da haste OA em torno de O e definida pela relação θ = (2 / π ) (sen π t), onde θ e t são expressos em radianos e segundos, respectivamente. O cursor B desliza ao longo da haste de tal form
Para o estudo do desempenho de um carro de corrida posiciona-se uma câmera filmadora de alta velocidade no ponto A. A câmera e montada em um mecanismo que possibilita que ela grave o movimento do carr