Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 161

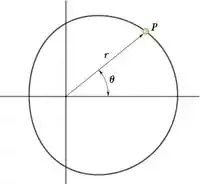
A trajetória de uma partícula P e um caracol de Pascal. O movimento da partícula e definido pelas relações r = b(2 + cos θ ) e θ = π t, onde t e θ são expressos em segundos e radianos, respectivamente. Determine (a) a velocidade e a aceleração da partícula quando t = 2 s, (b) o valor de θ para o qual a intensidade da velocidade e máxima.

Passo 1

E ai gurizada tudo bem? O enunciado pede que a gente encontre (a) a velocidade e a aceleração da partícula quando t = 2 s, (b) o valor de θ para o qual a intensidade da velocidade e máxima.

Então consideraremos:

r = b 2 + cos ⁡ π t         θ = π t

Então

r ˙ = - π b sin ⁡ π t         θ ˙ = π

e

r ¨ = - π 2 b cos ⁡ π t         θ ¨ = 0

Agora

v = r ˙ e r + r θ ˙ e θ = - π b sin ⁡ π t e r + π b 2 + cos ⁡ π t e θ

e

a = r ¨ - r θ ˙ 2 e r + r θ ¨ + 2 r ˙ θ ˙ e θ = - π 2 b cos ⁡ π t - π 2 b 2 + cos ⁡ π t e r

+ 0 - 2 π 2   b sin ⁡ π t e θ = - 2 π 2 b 1 + cos ⁡ π t e r + sin ⁡ π t e θ

Passo 2

  1. Em t = 2:

v = - 0 e r + π b 2 + 1 e θ

ou

a = - 2 π 2 b 1 + 1 e r + 0 e θ

Passo 3

Temos

v = π b ( - sin ⁡ π t ) 2 + ( 2 + cos ⁡ π t ) 2

= π b 5 + 4 cos ⁡ π t         θ = π t

= π b 5 + 4 cos ⁡ θ

Por observação,

v = v m a x         quando       cos ⁡ θ = 1

Resposta

a)       v = 3 π b e θ

a = - 4 π 2 b e r

b)   θ = 2 n π ,         n = 0 ,   1 ,   2 , …

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pequeno objeto é liberado a partir do repouso em um tanque de óleo. A aceleração de descida do objeto é g - k v , onde g é a aceleração constante devido à gravidade, k é uma constante que depende d
Uma cápsula impulsionada a vácuo para um sistema de transporte tubular de alta velocidade do futuro está sendo projetada para operação entre duas estações A e B , que estão distantes 10k m . Se a acel
A resistência aerodinâmica ao movimento de um carro é aproximadamente proporcional ao quadrado da sua velocidade. A resistência adicional ao atrito é constante, de modo que a aceleração do carro quand
Um velocista atinge sua velocidade máxima v m á x á em 2,5 segundos partindo do repouso com aceleração constante. Mantém então esta velocidade e termina 100 metros no tempo total de 10,40 segundos. De
O corpo caindo com velocidade v 0 colide e mantém contato com a plataforma apoiada por um jogo de molas. A aceleração do corpo após o impacto é a = g - c y , onde c é uma constante positiva e y é medi