Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 75
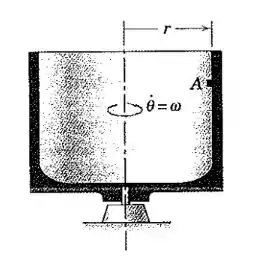
Um pequeno objeto é mantido contra a superfície vertical do recipiente cilíndrico rotativo de raio pela ação centrífuga. Se o coeficiente de atrito estático entre o objeto e o recipiente é , determine a expressão para a velocidade angular mínima do recipiente que impedirá o objeto de escorregar para baixo na superfície vertical.
Passo 1
A ação centrífuga vai “empurrar” a partícula contra a parede, e é essa a fora que vai manter o atrito entre os dois:
E sabemos que o módulo dessa “força” centrífuga é:
E então:
E essa força de atrito vai impedir que a partícula desliza para baixo pela parede, puxada pelo peso.
Passo 2
Isso quer dizer que para a partícula se manter em equilíbrio, precisamos de:
E então:
Pronto!
Resposta
A velocidade angular mínima é .
Exercícios de Livros Relacionados
3/59) As pequenas esferas são livres para se deslocar nasuperfície interna das câmaras esféricas rotativas rotativas mostradas em seção transversal com raio R = 200m m . Se as esferas atingem uma posi
3/51) Se o bloco de 2k g passa sobre o topo B da porção circular da trajetória com uma velocidade de 3,5m / s , calcule o módulo N B da força normal exercida pela trajetória sobre o bloco . Determine
3/55) O carro passa sobre o topo de uma curva num plano vertical em A com uma velocidade de 60k m / h e então passa pelo fundo de uma depressão em B . Os raios de curvatura da estrada em A e B são amb
3/57) O tubo vazado em torno do eixo horizontal que passa pelo ponto O e girano plano vertical com umavelocidade angular constante no sentido anti-horário θ ' = 3 r a d / s . Se uma partícula de 0,1k
3/63) Quando o esqueitista transpõe asuperfície mostrada , as velocidades do seu centro de massa em θ = 0 ° , 45 ° e 90 ° são 8,5m / s , 6m / s e 0 , respectivamente . Determine a força normal entre a