Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 144
Uma viga é submetida a uma carga distribuída linearmente em ordem decrescente e repousa em dois suportes largos e , que exercem cargas uniformemente distribuídas para cima como mostrado na figura. Determine os valores de e correspondente ao equilíbrio quando .
Passo 1
Pra começar podemos dividir o carregamento em duas regiões triangulares e calcular as reações em cada uma delas, dessa forma, com o auxílio do diagrama de corpo livre a seguir, temos:
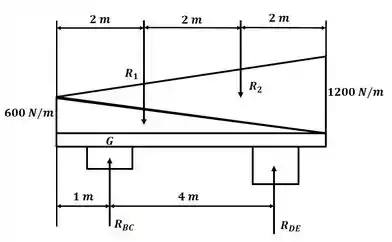
Passo 2
Beleza! Agora vamos aplicar o somatório de momentos em relação ao ponto para obter o valor do carregamento :
Isolando e resolvendo:
Passo 3
E, pra terminar, vamos aplicar o somatório de forças na direção para encontrar o valor do carregamento :
Isolando e substituindo o valor de encontrado no passo 2, temos:
Resposta
Exercícios de Livros Relacionados
Para a viga e o carregamento mostrados nas figuras, determine (a) a intensidade e a localização da resultante da carga distribuida, (b) as reações de apoio da viga.
Determine as reações de apoio da viga para o carregamento dado quando ω 0 = 2190N / m .
Determine as reações de apoio da viga para a carga dela.
Para a viga e o carregamento mostrados nas figuras, determine (a) a intensidade e a localização da resultante da carga distribuida, (b) as reações de apoio da viga.
Determine as reações de apoio da viga para a carga dela.