Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 7.Problemas - Ex. 112

Um comprimento de 50,5   m do arame tendo a massa por unidade de comprimento de 0,75   k g / m é usado em um vão de 50   m . Determine (a) a flecha aproximada do arame, (b) a tensão máxima no arame. [Dica: Use apenas o primeiro termo da equação (7.10)]

Passo 1

Bom galera, vamos começar esboçando o cabo pra facilitar nossa vida, fica mais ou menos assim:

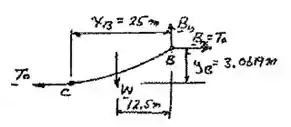
O problema pediu para a gente usar a equação 7.10 , então vamos calcular os dois primeiros termos da equação:

s B = 1 2 50,5 = 25,25   m

x B = 1 2 50 = 25   m

Passo 2

Show de bola, agora vamos usar a primeira parte da equação 7.10 :

s B = x B 1 + 2 3 y B x B 2

→ 25,25 = 25 1 + 2 3 h 25 2

→ 1 + 2 3 h 25 2 = 1,01

→ 2 3 h 25 2 = 0,01

h = 0,015 25 = 3,062   m

Passo 3

Então, a gente analisa a parte C B , mas primeiro vamos encontrar o peso:

W = s B ⋅ w

→ W = s B ⋅ ( 0,75 ⋅ 9,81 )

→ W = 25,25 ⋅ 7,3575

→ W = 185,78   N

Nós podemos analisar o momento, sabendo que o cabo encontra-se em equibrio:

∑ M B = 0

→ T 0 3,0619 - 185,78 12,5 = 0

Assim encontramos:

T 0 = 758,4   N

Logo:

B x = T 0 = 758,4   N

Passo 4

Então, analisamos as forças na horizontal:

∑ F y = 0

→ B y - 185,78 = 0

→ B y = 185,78   N

Por fim, nós fazemos o Pitágoras para encontrar a tensão máxima:

T m 2 = B x 2 + B y 2

→ T m = B x 2 + B y 2

→ T m = 758,4 2 + 185,78 2

→ T m = 781   N

Resposta

h = 3,062   m

T m = 781   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sendo θ o ângulo formado entre um cabo uniforme e a horizontal, mostre que, em qualquer ponto, (a) s = c tan ⁡ θ , (b) y = c sec ⁡ θ .
Determine a razão flecha por vão para a qual a tração máxima no cabo é igual ao peso total do cabo A B interno.
Um cabo A B de 3m é fixado em dois colares como mostra a figura. O colar em A pode deslizar livremente ao longo da haste; um batente de fixação na haste evita que o colar B se mova na haste. Desprezan
À esquerda do ponto B , o cabo longo A B D E repousa sobre a superfície horizontal áspera mostrada na figura. Sabendo que a massa por unidade de comprimento do cabo é 2k g / m , determine a força F qu
Resolva o Problema 7.147 considerando que o ângulo θ formado pela barra e pela horizontal é 45 ° .