Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 134
O tubo em ângulo reto é novamente mostrado aqui. Substitua a força trativa de que o cabo exerce no ponto por um sistema força-binário no ponto
Passo 1
Vamos transportar a força feita no ponto para o ponto , e também o momento feito pela força em torno dele. Primeiro calculamos o vetor de , e depois o momento por uma abordagem vetorial, utilizando a fórmula:
Sendo o veotr que aponta de para .
Passo 2
Olha só, primeiro vamos calcular o vetor da força. Fazemos isso multiplicando o módulo pelo vetor unitário que aponta de para , o vetor unitário é calculado da seguinte maneira:
Calculamos o vetor olhando para as distâncias entre e em cada direção:
Agora, calculando o módulo, vamos ter
Com isso encontramos o vetor unitário e a expressão do vetor
E nosso vetor será
Passo 3
Agora, calcularemos o momento em torno de . Primeiro precisamos do vetor :
Então fazendo o produto vetorial teremos
O produto vetorial é feito com o seguinte determinante
O determinante é resolvido da seguinte forma
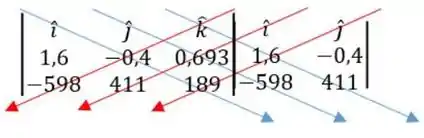
Os valores que estão representados em azul mantem o sinal, e os em vermelho devem ser multiplicados por . Sendo assim, vamos ter
Pronto, tá resolvido nosso problema.