Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 129

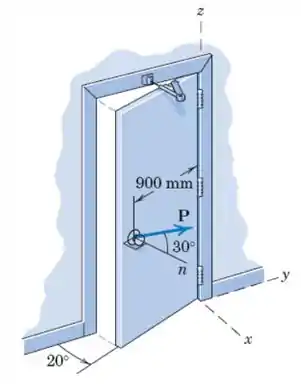
Ao se abrir uma porta que está equipada com um mecanismo de retorno, uma pessoa exerce uma força de módulo como mostrado. A força e a normal à face da porta estão em um plano vertical. Calcule o momento de em relação ao eixo .

Passo 1

Fala vocês, meus queridxs! Como vocês estão? Tudo certo por aí?

Se liguem só, apesar da cara de assustador desse problema ele é bem tranquilo de ser feito e a gente resolve ele sem nenhum problema sabe por quê? Porque se o problema é mau

Como a nossa força faz um ângulo de com a normal , que é ortogonal ao eixo , o momento em relação a esse eixo será dado por

Onde é a distância entre o ponto de aplicação da força e o eixo . Então, teremos

Pronto! Tá resolvido nosso problema. Não disse que ia só tinha a cara de assustador?

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para o sistema de duas forças do Prob. 2/157, determine as coordenadas do ponto no plano x - z por onde passa a linha de ação da resultante do sistema.

Substitua o sistema de duas forças e um binário mostrado no Prob. 2/158 por um torçor. Determine o módulo do momento M → do torçor, módulo da força R → da chave e as coordenadas do ponto P no plano x

Sabe-se que a força F da componente y exerce 90N no pino P , quando θ=30 ° e β=15 ° . Determine o módulo de força F e as componentes xd eF .

Um cabo esticado entre o suporte fixo AeB está sob uma tensão trativa de 2k N . Expresse a tensão como um vetor usando, os vetores unitários iej , primeiro, e como uma força T A atuando em A e como um

As três forças atuam perpendiculares à placa retangular, como mostrado. Determine os momentos M 1d eF 1 ,M 2d eF 2eM 3d eF 3 , todos em relação ao ponto O .