Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.2 - Ex. 40

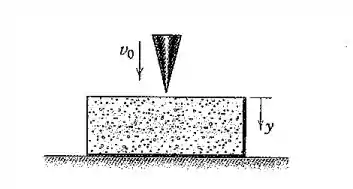
O cone caindo com uma velocidade v 0 atinge e penetra o bloco de material de embalagem . A aceleração do cone após o impacto é a = g - c y ² , onde c é uma constante positiva e y é a distância de penetração. Se a profundidade de penetração máxima observada é de y m , determine a constante c .

Passo 1

Depois que o cone cai sobre o bloco, ele sofre uma aceleração a no sentido contrário ao seu movimento até parar. O ponto onde ele para ( v = 0 ) é y = y m , ou seja:

y = y m         ⇒         v = 0

Para poder tirar proveito disso precisamos de uma relação entre a velocidade e a posição y . Vamos usar a definição de aceleração:

a = d v d t = d v d y d y d t = v d v d y

a   d y = v   d v

Passo 2

Substituindo com a fórmula para a nessa equação diferencial:

g - c y 2 d y = v   d v

E integrando dos dois lados:

∫ 0 y m á x g - c y 2 d y =   ∫ v 0 0 v   d v

Perceba que a velocidade vai do valor inicial v 0 até zero enquando a posição vai de zero até y = y m á x .

Resolvendo essas integrais encontramos o seguinte:

g y m á x - c 3 y m á x 3 = - 1 2 v 0 2

E agora é só isolar a constante c :

6 g y m á x - 2 c y m á x 3 = - 3 v 0 2

c = 3 v 0 2 + 6 g y m á x 2 y m á x 3

Resolvido!

Resposta

A constante c vale 3 v 0 2 + 6 g y m á x 2 y m á x 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

29. A posição de uma partícula ao longo de uma linha reta é dada por s = 1,5 t 3 - 13,5 t 2 + 22,5 tm , onde t é dado em segundos. Determine a posição da partícula quando t = 6 s e a distância total q
31.A aceleração de uma partícula à medida que se move ao longo de uma linha reta é dada por a = 2 t - 1m / s 2 , onde t é dado em segundos. Se s = 1m e v = 2m/s quando t = 0, determine a velocidade da
35. Uma partícula tem velocidade escalar inicial de 27 m/s. Se ela experimenta uma desaceleração de a = - 6 tm / s 2 , onde t é dado em segundos, determine sua velocidade após ela ter viajado 10m. Qua
28. Se os efeitos da resistência atmosférica são levados em consideração, um corpo caindo tem uma aceleração definida pela equação a = 9,81 1 - v 2 10 - 4 m s 2 , onde v é dado em m/s e a direção posi
41. Uma partícula está se movendo ao longo de uma linha reta de maneira que sua posição de um ponto fixo é s = 12 - 15 t 2 + 5 t 3m , onde t é dado em segundos. Determine a distancia total percorrida