Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 24

Os membros AB e BE de treliça mostrada são de barras de aço ( E = 200 G P a ) com 25   m m de diâmetro. Para o carregamento mostrado, determinar o alongamento de ( a ) barra AB; ( b ) barra BE

Passo 1

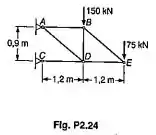
Vamos começar desenhando a treliça e as reações de apoio. Note que no Ponto C só é possível força horizontal.

Então vamos calcular as reações de apoio. Podemos encontrar a reação em C com o somatório de momentos em A.

∑ M A = 0 ⇒ R C X ⋅ 0,9 - 150 ⋅ 1,2 - 75 ⋅ 2,4 R C X = 150 ⋅ 1,2 + 75 ⋅ 2,4 0,9 = 400   k N

Com o somatório de forças na direção X podemos calcular a reação horizontal em A

∑ F X = 0 ⇒ - R A X + R C X = 0 R A X = 400   k N

E com o somatório de forças na direção Y calculamos a reação vertical em A

∑ F Y = 0 ⇒ R A Y - 150 - 75 = 0 R A Y = 225   k N

Passo 2

Antes de começar a calcular a força na treliça, precisamos calcular algumas propriedades geométricas: o ângulo entre as barras e o tamanho da barra inclinada.

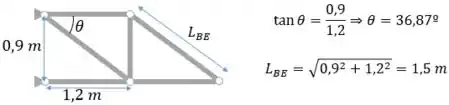
Para poder calcular o alongamento, precisamos da área de seção transversal:

A = π d 2 4 = π ⋅ ( 25   m m ) 2 4 = 156,25 π   m m 2

Passo 3

Agora vamos usar o método dos nós para encontrar as forças nos elementos. Primeiro vamos calcular o nó A:

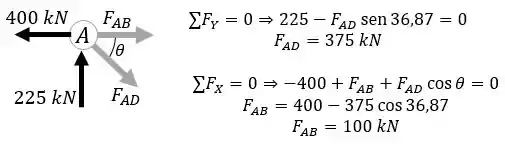
E agora podemos calcular as forças no nó B. Mas não precisamos calcular todas as forças, apenas a força F B E que atua na barra   B E :

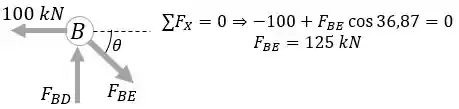
Passo 4

Agora temos todos as forças que nos interessam. Utilizando a Equação 2.7 do livro, vamos calcular a deformação nas barras AB e BE:

δ A B = F A B L A B A E = 100   k N ⋅ 1,2   m 156,25 π   m m 2 ⋅ 200   G P a = 1,222 ⋅ 10 - 3   m

δ B E = F B E L B E A E = 125   k N ⋅ 1,5   m 156,25 π   m m 2 ⋅ 200   G P a = 1,910 ⋅ 10 - 3   m

Resposta

  1. δ A B = 1,222 ⋅ 10 - 3   m
  2. δ B E = 1,910 ⋅ 10 - 3   m
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cada uma das barras da treliça tem área de seção transversal de 780 m m ² ². Se a tensão normal média máxima em qualquer barra não pode ultrapassar 140M P a , determine o valor máximo P das cargas que
Cada uma das barras da treliça tem área de seção transversal de 780mm². Determine a tensão normal média em cada elemento resultante da aplicação da carga P = 40 kN. Indique se a tensão é de tração ou
O gancho é usado para sustentar o tubo de tal modo que a força no parafuso vertical é 775N . Determine a tensão normal média desenvolvida no parafuso B C se ele tiver diâmetro de 8m m . Considere que
O bloco de concreto tem as dimensões mostradas na figura. Se o material falhar quando a tensão normal média atingir 0,84 MPa, determine a maior carga vertical P aplicada no centro que ele pode suporta
A luminária de 250N é sustentada por três hastes de aço interligadas por um anel em A . Determine qual das hastes está submetida à maior tensão normal média e calcule seu valor. Considere θ=30 ° . O d