Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 68
A barra rígida suporta um carregamento distribuído uniforme de Determine a força em cada cabo se cada um tiver área de seção transversal de e .
Passo 1
Uma barra está apoiada em um pino em e por dois cabos em e . Um carregamento uniformemente distribuído é aplicado sobre a barra, fazendo-a girar ao redor de .
Características dos cabos:
- Módulo de elasticidade:
- Área: .
- Comprimento inicial: .
O carregamento atua de cima pra baixo com distribuído uniformemente em .
Quando a barra girar ao redor de no sentido horário, os cabos e vão resistir com forças e .
Queremos saber o valor dessas forças!
Passo 2
Diagrama de corpo livre.
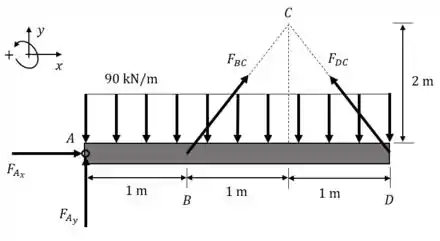
Vamos fazer o equilíbrio de momentos ao redor de , assim as reações e não contribuem e não precisamos nos preocupar com elas.
Atenção que a força equivalente pra esse carregamento é de atuando a de .
O ângulo é aquele formado com a horizontal pelas forças inclinadas.
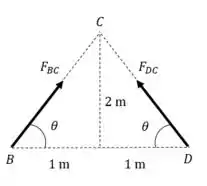
Temos duas incógnitas e uma equação. Não adianta vermos o equilíbrio de forças porque só vai adicionar mais incógnitas ( e ).
A condição de compatibilidade vai ter que nos dar outra equação!
Passo 3
A condição de compatibilidade dessa questão tem vários detalhes, vamos com calma.
Queremos relacionar as forças e , e sabemos que os fios vão ser esticados: vai aumentar um e aumenta . A fórmula que temos pra relacionar força com deslocamento é essa:
Beleza, vejamos como as cordas são deformadas. A barra é rígida e vai girar ao redor de . Lembrando que estamos considerando pequenas deformações, veja a figura.
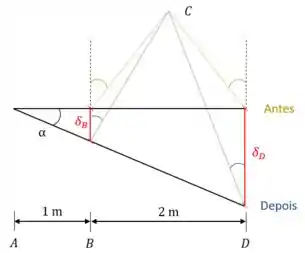
Os deslocamentos marcados, e , são o quanto os pontos e desceram após a rotação da barra (linha preta). Podemos relacioná-los usando a tangente do ângulo :
Nós achamos uma relação entre deslocamentos da barra, porém estamos procurando deslocamentos das cordas. Veja na figura anterior como as cordas se esticam ao se manterem presas em e . Precisamos relacionar com e com para podermos continuar.
Passo 4
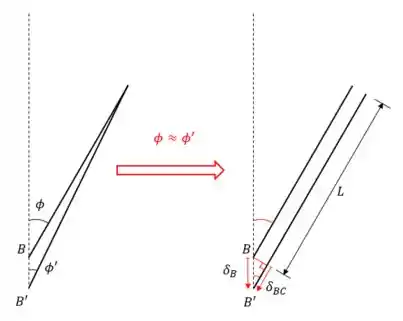
Com o giro da barra, o ponto vai descer, então em tese o ângulo na figura vai mudar para algum . Mas como estamos sempre assumindo pequenas deformações, essa mudança no ângulo é desprezível: .
Com a aproximação, as retas são praticamente paralelas, e aí o aumento da corda (reta inclinada) aparece como na figura acima. Escrevemos
Confira que nas figuras, então .
Como a corda faz o mesmo ângulo com a horizontal, vai acontecer exatamente igual (mas isso não é sempre o caso, cuidado!):
Passo 5
Agora é só voltar de equação em equação até achar as forças.
Essa equação acima é finalmente a condição de compatibilidade da questão! Agora vamos pras forças:
Passo 6
Use na equação do equilíbrio de momentos:
Resposta
Força na corda :.
Força na corda :.