Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 69
A posição original da barra rígida é horizontal e ela é sustentada por dois cabos com área de seção transversal de 36 mm² cada e E = 200 GPa. Determine a leve rotação da barra quando uma a carga uniforme é aplicada.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos??
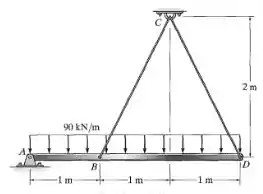
O que está acontecendo ali? Antes do carregamento, essa viga está como na figura. Aquele triângulo formado pelos dois cabos é simétrico.
Depois do carregamento, há alongamento nesses cabos. Como o carregamento não é simétrico, um cabo vai alongar mais que o outro, causando uma rotação nessa barra. O ângulo dessa barra carregada em relação a horizontal é o que queremos descobrir.
Nosso primeiro passo será trazer TODOS os nossos dados do desenho pra cá.
Agora, vamos analisar a distância para de e para o ponto C e suas relações.
Vamos observar também que o ângulo em relação a horizontal e o ponto é de (já que os catetos valem 2).
Com isso em mente, vamos achar as forças nos cabos e seus alongamentos. Bora!
Passo 2
Nosso DCL fica:
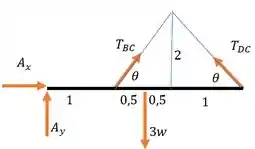
Precisamos de duas equações que relacionam esses ’s para achar essas tensões.
Primeiro, usamos somatório de momento em :
Passo 3
A outra vai ser achada pela compatibilidade de deslocamentos. Nossa viga é rígida. Então ela não pode curvar, só rotacionar. Como o alongamento dos cabos ocorre algo assim:
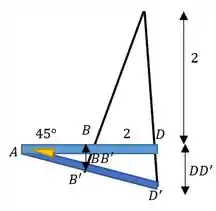
Por semelhança de triângulos, podemos escrever:
Mas quem são esses valores? Eles são as projeções dos nossos deslocamentos na vertical. Se a gente supor que ângulo entre cabos ficou de , então podemos escrever:
Lembrando da fórmulinha para deslocamento:
Daí:
Prontinho, mas uma equação.
Passo 4
Vamos olhar para o nosso desenho de novo:
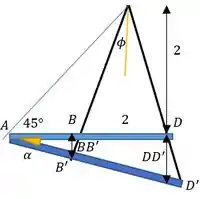
O ângulo de rotação que a questão pede é . Para achar ele a gente pode ou achar ou, não precisamos dos dois! Então vamos achar só .
Para achar essa tensão, usamos as duas equações que montamos:
Passo 5
Voltando para as continhas:
Ficamos com esse triângulo:
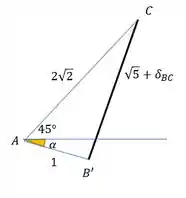
Aí achamos pela lei dos cossenos:
Isolando :
Obs: Ficou diferente do gabarito do livro, mas tá certinho, tá?