Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 4.Problemas - Ex. 11

O conjunto é composto por três hastes de titânio ( T i   - 6 A 1 - 4 V ) e uma barra rígida A C . A área da seção transversal de cada haste é dada na figura. Se uma força de 30   k N for aplicada ao anel F , determine o deslocamento horizontal do ponto F .

Passo 1

E aí?

Desejamos encontrar o deslocamento horizontal do ponto F e para isso devemos notar, primeiramente, que como o material tratato é o T i   - 6 A 1 - 4 V seu módulo de elasticidade é tabelado e dado por E = 120   G P a ,

Além disso, devemos lembrar que o alongamento vai ser calculado a partir da seguinte fórmula

δ = F o r ç a   a p l i c a d a ⋅ ( c o m p r i m e n t o   e m   a n á l i s e ) M o d .   d e   e l a s t i c i d a d e ⋅ ( Á r e a   e m   a n á l i s e ) = P L E A

Passo 2

Das forças internas nas hastes vamos ter

∑ M a = 0 → F c d ⋅ 0,9 m - 30 k N ⋅ 0,3 m = 0 → F c d = 10,0   k N

∑ F y = 0 → F c d + F a b - P = 0 → F a b = 20   k N

Passo 3

Calculadas as forças acima, podemos encontrar alguns deslocamentos que servirão de base para que possamos encontrar o deslocamento exatamente em F que vai ser dada por uma combinação de deslocamentos.

Assim, aplicando a fórmula descrita no primeiro passo vamos ter

δ c = F C d ⋅ 1,2 m E ⋅ A c d ≈ 0,1667   m m   e   δ a = F a b ⋅ 1,8 m E ⋅ A a b ≈ 0,3333   m m  

Passo 4

O deslocamento em E , podemos achar por semelhança de triângulos. Repara:

δ a - δ b δ e - δ e = 0,9 0,6

δ e ≈ 0,2778   m m

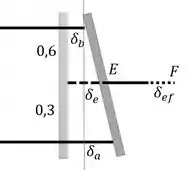
Mas repara que até chegar no ponto F , temos outro haste. Então ela também sofre alongamento.

δ F - E = P ⋅ 0,3 m E ⋅ A e f ≈ 0,0625   m m

Por fim, o deslocamento exatamente no ponto F será dada por esse alongamento da haste E F mais o deslocamento em E :

δ F = δ E + δ F - E = 0,340278   m m

Resposta

δ F = 0,340278   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O conjunto é composto por três hastes de titânio e uma barra rígida A C . A área da seção transversal de cada haste é dada na figura. Se uma força vertical P=20k N for aplicada ao anel F , determine o
O poste é feito de abeto Douglas e tem diâmetro de 60m m . Se estiver sujeito a uma carga 20k N e o solo proporcionar resistência ao atrito uniformemente distribuída ao longo do comprimento do poste e
O sistema articulado é composto por três elementos de aço A - 36 conectados por pinos, cada um com área de seção transversal de 500m m 2 . Determine o valor da força P necessária para deslocar o ponto
A coluna é construída de concreto de alta resistência e seis hastes de reforço de aço A - 36 . Se for submetida a uma força axial de 150k N , determine o diâmetro exigido para cada haste, de modo que
O tubo de aço A-36 tem raio externo de 20m m e raio interno de 15m m . Se ele se ajustar exatamente entre as paredes fixas antes de ser carregado, determine a reação nas paredes quando for submetido à