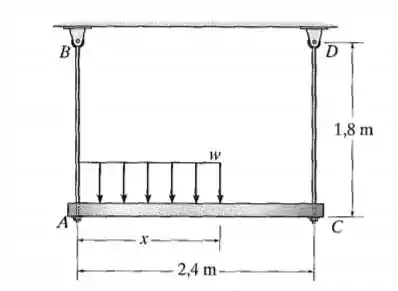
A viga rígida está apoiada em suas extremidades por dois tirantes de . Se a tensão admissível para o aço for , a carga e , determine o diâmetro de cada haste de modo que a viga permaneça na posição horizontal quando carregada.
Passo 1
Desejamos encontrar o diâmetro das hastes de forma que a viga continue na posição horizontal mesmo que carregada. Tomemos então as forças internas nas hastes (adotando o sentido anti-horário como positivo) e teremos
Passo 2
Para que barra continue na posição horizontal devemos ter um alongamento igual nas hastes . Além disso, por se tratar de diâmetro temos que as áreas dos pinos serão dadas por
Então
De tiramos que
Passo 3
Por fim, se assumirmos falha nas hastes vamos ter
Como