Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 94

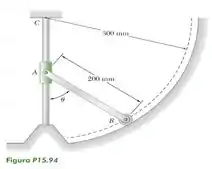
A barra AB é fixada ao colar em A e é equipada com uma pequena roda em B. Sabendo que quando θ = 60 ° a velocidade do colar é 250   m m / s para cima, determine (a) a velocidade angular da barra AB, (b) a velocidade do ponto B.

Passo 1

Bora pra questão 94 agora, meus caros (as)!

E já sabe, né! Nada melhor do que uma figura pra ajudar a entender uma questão.

Vamos fazer um esboço destacando vetorialmente as velocidades e o centro de rotação instantâneo desse sistema. Aqui está, nossa bela imagem...

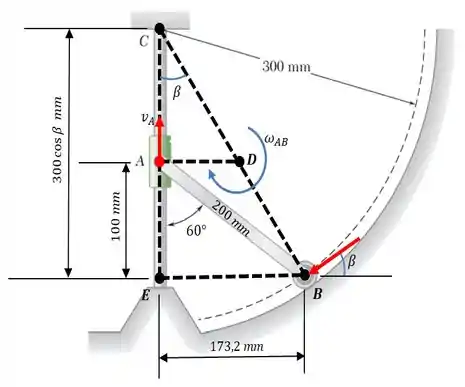
Passo 2

a) Bom! Inicialmente, a gente tem que determinar a velocidade angular da barra A B , que chamaremos de ω A B .

D é centro de rotação instantâneo, na figura que desenhamos. E o enunciado nos dá o valor da velocidade v A do colar de 250   m m / s e para cima...

v A = 250   m m / s   ↑

Sendo assim, temos que...

v A = A D ω A B

Como a gente já sabe v A ! Vamos atrás de A D !

Passo 3

Se liga! Com base na figura esboçada, temos que...

sen ⁡ β = 173,2   m m 300   m m

Sendo assim...

β = sen - 1 ⁡ 173,2   m m 300   m m

β = sen - 1 ⁡ 0,57

β = 35,264 °

Uma vez obtido β , o valor de C E será igual à...

C E = 300 cos ⁡ β  

C E = 300 cos ⁡ 35,264 °   m m

C E = 244,95   m m

Logo, A C vai valer...

A C = C E - A E

A C = 244,95 - 100

A C = 144,95   m m

E aí pra determinar A D , como já sabemos o valor de β , bora usar a tangente...

tan ⁡ β = A D A C

A D = A C tan ⁡ β

A D = ( 144,95   m m ) tan ⁡ β

A D = 102,49   m m

Passo 4

Pronto! Já temos A D !

Isolando ω A B na fórmula do P a s s o   2 :

ω A B = v A A D

ω A B = 250   m m / s 102,49   m m

ω A B = 2,44   r a d / s   ⤸

No sentido horário, porque v A tende a fazer a barra A B girar nesse sentido!

Passo 5

b) Agora é a vez de obter a velocidade do ponto B , v B !

Pela imagem do P a s s o   1 , temos que...

v B = B D ω A B

Bom! Precisamos do B D ! É o único dado que tá faltando!

Pois muito bem! Olhando a nossa imagem, temos que...

B D = B C - C D

B C a gente sabe que vale...

B C = 300   m m

Já C D vai ser dado, uma vez que temos o valor de β , por...

C D = A C cos ⁡ β

C D = 144,95   m m cos ⁡ 35,264 °

C D = 177,53   m m

Logo,

B D = B C - C D

B D = 300   m m - 177,53   m m

B D = 122,47   m m

E então...

v B = B D ω A B

v B = 122,47   m m ( 2,44   r a d / s )

v B = 298,83   m m / s

v B ≅ 299   m m / s

Essa velocidade faz um ângulo β com a horizontal. Desse modo, escrevendo em módulo e ângulo...

v B ≅ 299   m m / s   ⦫ 35,3 °

Resposta

a)

ω A B = 2,44   r a d / s   ⤸

b)

v B ≅ 299   m m / s   ⦫ 35,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A viga esbelta de 3m possui uma massa de 50k g e é liberada a partir do repouso na posição horizontal em θ = 0 . Se o coeficiente de atrito estático entre o suporte fixo junto a O e a viga é de 0,30 ,
11. Se a barra AB desliza ao longo da ranhura horizontal com uma velocidade de 18 m/s, determine a velocidade angular da barra de ligação BC no instante mostrado.
Para o instante representado, o centro instantâneo de velocidade nula para a placa retangular em movimento plano está localizado em C. Se a placa possui uma velocidade angular no sentido anti-horário
A placa retangular gira em torno de seu eixo fixo z. No instante considerado sua velocidade angular é ω = 3r a d / s e está diminuindo na taxa de 6 rad/s por segundo. Para esse instante escreva as exp
O grande carretel para cabo de eletricidade é rolado para cima no plano inclinado pelo veículo conforme mostrado. O veículo parte do repouso com x = 0 para o carretel e acelera na taxa constante de 0,