Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 15.Problemas - Ex. 90

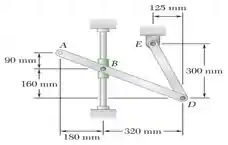
O braço ABD está conectado por pinos ao colar em B e à manivela DE. Sabendo que a velocidade do colar B é de 400   m m / s para cima, determine (a) a velocidade angular do braço ABD e (b) a velocidade do ponto A.

Passo 1

Bora pra questão 90 agora, meus caros(as)!

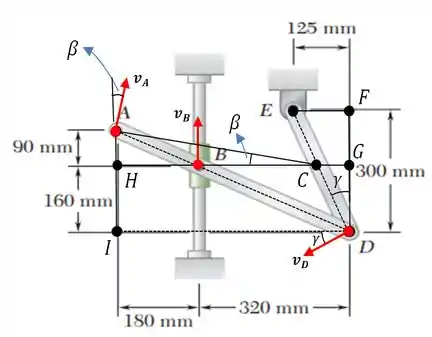
E já sabe, né! Vamos começar fazendo um esboço do sistema, no caso o braço A B D , representando vetorialmente as velocidades e destacando o centro de rotação instantâneo...

Passo 2

a) Bom! Inicialmente, a gente tem que obter a velocidade angular do braço A B D !

Pois muito bem! C   é o centro de rotação instantâneo do braço A B D !

A questão nos diz que a velocidade do colar B é de 400   m m / s para cima, ou seja...

v B = 400   m m / s   ↑

Baseado nisso, ao olhar a figura do enunciado, temos que v B vai ser dado pela seguinte fórmula...

v B = C B ω A B D

Passo 3

Vamos então tratar de obter C B .

Sabemos pela imagem, que...

C B + C G = 320   m m

E o ângulo γ é dado por...

γ = tan - 1 ⁡ 125 300

γ = 22,62 °

Logo, podemos obter C G usando a relação abaixo...

tan ⁡ γ = C G D G

C G = D G tan ⁡ γ = D G ⋅ tan ⁡ γ

C G = 160   m m ⋅ tan ⁡ γ

C G = 160   m m ⋅ tan ⁡ 22,62 °

C G = 66,67   m m

Sendo assim...

C B = 320   m m - 66,67   m m

C B = 253,33   m m

Obtido C B , vamos voltar á formula do P a s s o   2 ...

v B = C B ω A B D

Isolando ω A B D e substituindo os valores numéricos...

ω A B D = v B C B

ω A B D = 400   m m / s   253,33   m m

ω A B D = 1,579   r a d / s   ⤾

Que está no sentido horário, pois v B tende a fazer o braço girar nessa direção!

Passo 4

b) Agora, vamos tratar de obter o valor de v A !

Pela figura, temos que...

v A = A C ω A B D

Vamos então tratar de obter A C .

Sabemos pela imagem, que...

H C + C G = 500   m m

E podemos obter C G usando a relação abaixo...

tan ⁡ γ = C G D G

C G = D G tan ⁡ γ = D G ⋅ tan ⁡ γ

C G = 160   m m ⋅ tan ⁡ γ

C G = 160   m m ⋅ tan ⁡ 22,62 °

C G = 66,67   m m

Sendo assim...

H C = 500   m m - 66,67   m m

H C = 433,33   m m

Passo 5

Obtido H C , para achar A C é só olhar a figura do P a s s o   1 e ver que...

cos ⁡ β = H C A C

Sendo que o valor de β   é igual à...

β = tan - 1 ⁡ A H H C = tan - 1 ⁡ 90   m m 433,33   m m

β = tan - 1 ⁡ 90   m m 433,33   m m

β = 11,733 °

β = 26,57 °

Logo, A C   vai valer...

A C = H C cos ⁡ β

A C = 433,33   m m cos ⁡ 11,733 °

A C = 442,58   m m

Aí sim, meus colegas! Demorou mais chegou!

Já podemos obter o valor de v A , que vai ser igual à...

v A = A C ω A B D

v A = 442,58   m m ( 1,579   r a d / s )

v A = 698,83   m m / s ≅ 699   m m / s

E essa velocidade faz um ângulo com a horizontal igual à...

90 ° - β = 90 ° - 11,733 ° = 78,267 °

90 ° - β ≅ 78,3 °

Sendo assim, em módulo e ângulo, chegamos ao seguinte resultado...

v A ≅ 699   m m / s   ∠   78,3 °

Terminamos aqui! Até a próxima!

Resposta

a)

ω A B D = 1,579   r a d / s   ⤾

b)

v A ≅ 699   m m / s   ∠   78,3 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

54. O pinhão A roda sobre a cremalheira fixa B com uma velocidade angular ω = 4 r a d s . Determine a velocidade da cremalheira C.
O anel semicircular uniforme de massa m = 2,5k g e raio médio r = 200m m está montado sobre raios de massa desprezível e gira em torno de um eixo horizontal através de O . Se o anel é liberado a parti
O cilindro maciço homogêneo possui uma massa de 100k g e está montado em um eixo em ângulo reto que gira livremente em torno do eixo horizontal O - O . Se o cilindro é liberado a partit do repouso com
A massa da engrenagem A é de 20k g e seu raio de giração centroidal é de 150m m . A massa da engrenagem B é de 10k g e seu raio de giração centroidal é de 100m m . Calcule a aceleração angular da engr
O anel semicircular de massa m e raio r está soldado no eixo vertical, que permite que o anel gire no plano horizontal em torno do eixo O - O . Se um torque M é aplicado ao anel por meio de seu eixo,