Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 6.Problemas - Ex. 117
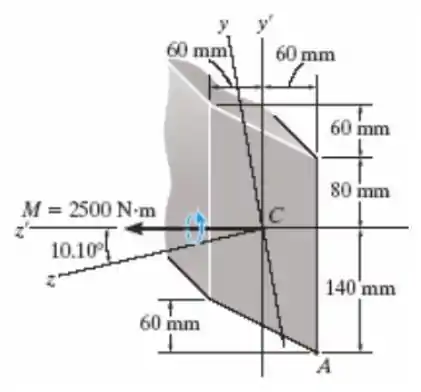
Para a seção, Iy’ = 31,7(10-6)m4, 12, Iz’ = 114(10-6)m4, Iy'z' = 15,1(10-6)m4. Usando as técnicas apresentadas no Apêndice A, a área da seção transversal do elemento tem momentos principais de inércia IY = 29,0(10-6)m4 e Iz= 117(10-6)m4, calculados em torno dos eixos principais de inércia y e z, respectivamente. Se a seção for submetida a um momento M = 2.500 N · m direcionado como mostra a figura, determine a tensão produzida no ponto A.
Passo 1
Faaaala, meu povo bonito!! Tudo bem com vocês?? Nossa questão de hoje já chegou fazendo carinho e nos dando os principais elementos da noite: os momentos de inércia, tanto para o eixo cartesiano clássico, quanto para o eixo rotacionado de 10,10º. O que ele nos pede é para calcular a tensão produzida no ponto A quando essa seção receber um momento aplicado na horizontal igual a 2500 N.m. Sacou??
Passo 2
Primeira coisa que vamos fazer aqui é usar a geometria analítica para encontrar a equação da reta para achar as coordenadas de A, já que os eixos estão fora do eixo (entenderam a piada?? Kkkkk Não?? Ok, vamos voltar).
Quando igualamos , temos o ponto de intersecção das retas em
Se substituirmos x em y, vamos encontrar o ponto de intersecção das retas em
Agora, depois de tanta reta de um lado pro outro, vamos fazer o módulo da distância entre o ponto A e a intersecção com y, nos dando sua nova coordenada.
Assim, achamos que o ponto A (60 mm, -140 mm) está a distante da intersecção das retas y e yA de:
Pera, esse valor é igual à coordenada z do ponto A!!
Passo 3
Pronto, agora não temos mais mistério. Já temos as novas coordenadas do ponto A e os momentos de inércia que o problema nos deu, agora só falta achar os momentos para cada eixo.
Sabemos que a tensão resultante será a soma de cada uma das componentes dos momentos de cada eixo. Sendo assim:
σ= -(M_z y)/I_z +(M_y z)/I_y =2,6 MPa