Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 1.Problemas - Ex. 37

Determine o valor da integral ∫ S A ∙ d a , onde A = (x2 + y2 + z2)(xi + yj + zk) e a superfície S é definida pela esfera R2 = x2 + y2 + z2. Calcule a integral diretamente e também utilizando o teorema de Gauss.

Passo 1

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de matrizes, vetores e cálculo vetorial.

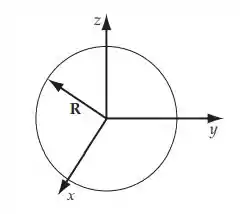
Para fazer a integral diretamente, observe que A = R 3 e r , na superfície, e que d a = d a e r .

∫ S A ∙ d a = R 3 ∫ S d a = R 3 4 π R 2 = 4 π R 5

Para usar o teorema da divergência, precisamos calcular ∇ ∙ A . Isso é feito melhor em coordenadas esféricas, onde A = r 3 e r . Usando o Apêndice F, vemos que:

∇ ∙ A = 1 r 2   ∂ ∂ r r 2 A r = 5 r 2

Portanto:

∫ V ∇ ∙ A d v = ∫ 0 π s e n   θ d θ ∫ 0 2 π d φ ∫ 0 R r 2 5 r 2 d r =

= R 5 ∫ 0 π s e n   θ d θ ∫ 0 2 π d φ = 2 π R 5 ∫ 0 π s e n   θ d θ = 2 π R 5 - cos ⁡ π + cos ⁡ 0 = 4 π R 5

Resposta

Ver passo a passo.

Exercícios de Livros Relacionados

Decomponha F2 nas componentes que atuam ao longo dos eixos u e v e determine suas intensidades.Fonte: Estática Mecânica para Engenharia – 14ª ed
Determine a intensidade e a direção da resultante F R=F 1+F 2+F 3 das três forças encontrando primeiro a resultante F ’=F 1+F 2 e depois formando F R=F ’+F 3 .Fonte: Estática Mecânica para Engenharia
Duas forças atuam sobre o parafuso de argola. Se F 1 = 400 N e F 2 = 600 N, determine o ângulo u ( 0 0 ≤u ≤180 0 ) entre elas, de modo que a força resultante tenha uma intensidade F R = 800 N.
Determine a intensidade e a direção da força resultante F R medida em sentido anti-horário a partirdo eixo x positivo. Resolva o problema encontrando primeiro a resultante F ’=F 1+F 2 e depois formand
Determine a intensidade e a direção da força resultante F R medida em sentido anti-horário a partirdo eixo x positivo. Resolva o problema encontrando primeiro a resultante o F ’=F 2+F 3 e depois forma