Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas de Revisão - Ex. 168

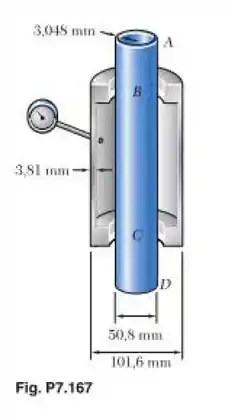
Para a montagem do Prob. 7.167, determine a tensão normal na jaqueta (a) na direção perpendicular ao eixo longitudinal da jaqueta, (b) na direção paralela a esse eixo.

Passo 1

Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos começar pela letra (a), calculando a tensão normal na jaqueta na direção perpendicular ao eixo longitudinal da jaqueta, para isso vamos utilizar a equação para a tensão em um vaso de parede fina, dada por:

σ = p r t

Em que p é a pressão manométrica, r é o raio interno e t é a espessura do vaso. Agora, para a letra (b), vamos precisar calcular um somatório de forças na direção y, para poder encontrar uma expressão para a tensão nessa direção. Então bora lá!

Passo 2

Beleza! Vamos começar calculando o valor do raio interno r para poder utilizar a equação da tensão descrita no passo 1. Então teremos:

r = 0,1016 2 - 0,00381 → r = 0,04699   m

Então, substituindo os valores conhecidos, temos:

σ = 3448.10 3 0,04699 0,00381 → σ = 42,5   M P a

Passo 3

Agora para a letra (b), precisamos aplicar o equilíbrio de forças na direção y para poder encontrar uma expressão para σ nessa direção. Faremos isso analisando a parede da jaqueta, para que ela fique em equilíbrio nessa direção, a força gerada pela pressão na área circular referente ao final do tubo interno até a sua parede (que chamaremos de força interna) deve ser igual a força na espessura da parede, ou seja:

F i = F p → p A i = σ A p → σ = p A i A p

Então precisamos calcular a área interna e a área da parede da jaqueta. Começando pela área interna, teremos:

A i = π r o 2 - r i 2 = π 0,04699 2 - 0,0508 2 2 → A i = 4,91.10 - 3   m 2

Agora, a área da parede da jaqueta será dada por:

A p = π r o 2 - r i 2 = π 0,1016 2 2 - 0,04699 2 → A p = 1,17.10 - 3   m 2

Então agora podemos substituir os valores conhecidos na equação para a tensão, onde chegaremos em:

σ = 3448.10 3 4,91.10 - 3 1,17.10 - 3 → σ = 14,46   M P a

Belezaaa!! Terminamos mais um, valeeeu!

Resposta

a :   σ = 42,5   M P a

b :   σ = 14,46   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um reservatório de pressão esférico tem um diâmetro externo de 5 m e espessura de parede de 24 mm é feito de um aço para o qual E = 200 GPa e ν = 0,29. Sabendo que a pressão manométrica no reservatóri
Determine a tensão normal em uma bola de basquete de 300 mm de diâmetro externo e espessura de parede de 3,0 mm que é inflada a uma pressão manométrica de 120 kPa.
O tanque de armazenagem cilíndrico não pressurizado indicado na figura tem uma parede com espessura de 5 mm e é feito de aço com um limite de resistência de 400 MPa na tração. Determine a altura máxim
Um vaso de pressão esférico, com diâmetro externo de 750 mm, deve ser fabricado com um aço que tem um limite de tensão σ L = 400M P a . Sabendo que se deseja um coeficiente de segurança de 4 e que a p
Para o tanque de armazenagem do Problema 7.104, determine a tensão normal máxima e a tensão de cisalhamento máxima na parede cilíndrica quando o tanque estiver totalmente cheio (h = 14,5 m).