Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 84
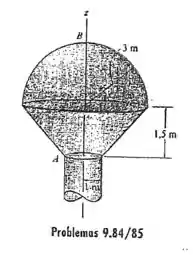
9.84 Determine a área da superfície de até do tanque.
Passo 1
Vamos separar o tanque em dois pedaços, a metade de uma esfera que fica em cima e o tronco de um cone que fica embaixo. A fórmula para determinar a área superficial é:
Onde é o ângulo de revolução em radianos
é a distância perpendicular do eixo de revolução ao centroide da curva de geração
e é o comprimento da curva de geração.
A metade de cima é formada pela revolução desse arco:
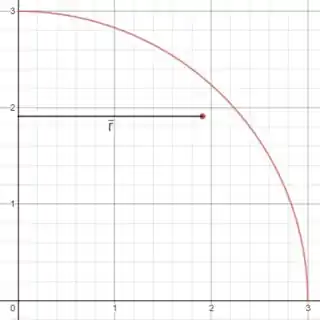
Esse arco é um quarto de uma circunferência, então podemos observar na tabela do apêndice que a distância é
O raio da circunferência é 3, logo
O comprimento do arco é igual a um quarto de circunferência:
E , porque o arco da uma volta completa para formar o tanque.
Então a área vai ser igual a:
Passo 2
Já a metade de baixo é formada pela revolução completa de um segmento de reta. Seu centroide é mais de achar, pois ele fica bem no meio da reta:
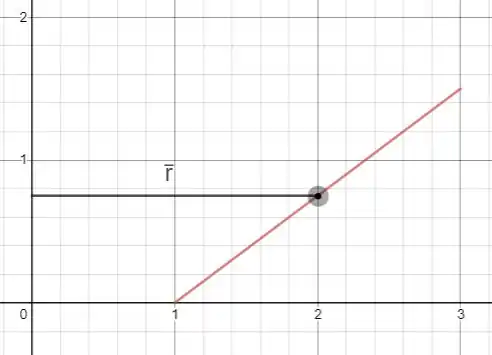
A distância vai ser igual a
A distância podemos encontrar por pitagoras:
Agora só multiplicar os valores:
Passo 3
Somando as duas áreas, vamos obter a área total: