Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.7 - Ex. 161

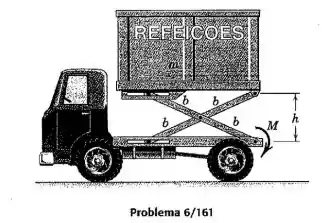
O contêiner do caminhão de entrega de alimentos para o suprimento de aeronaves tem uma massa m quando está carregado e é elevado por meio da aplicação de um momento M na extremidade inferior da barra que é articulada ao chassi do caminhão. As ranhuras horizontais permitem que o mecanismo se estenda enquanto o contêiner é elevado. Determine a aceleração ascendente do contêiner em termos de h , para um determinado valor de M . Despreze a massa das barras.

Passo 1

Seja θ o ângulo formado entre a barra e a horizontal. Por geometria, é possível concluir que

h = 2 b × s e n θ

Isolando s e n θ , temos

s e n θ = h 2 b

Sabemos que

c o s 2 θ + s e n 2 θ = 1

De onde tiramos

c o s θ = 1 - h 2 b 2 2  

Passo 2

A variação diferencial na energia cinética equivale ao trabalho diferencial realizado sobre o sistema pelas forças reultantes. Assim, para a energia cinética, temos

d T = m × a × d h = m × a × d 2 b s e n θ = 2 m × b × a × c o s θ d θ

Já a variação da eneria potencial gravitacional do sistema é dada por

d V g = m × g × d h = 2 m × b × g ×   c o s θ d θ

Passo 3

Sabemos que para um intervalo infinitesimal de movimento, a relação Trabalho-Energia é dada por

d U ' = d T + d V g

Além disso, para rotações finitas

d U ' = M d θ

Igualando as duas equações, ficamos com

d T + d V g = M d θ

Substituindo as expressões encontradas, temos

2 m × b × ( a + g ) × 1 - h 2 b 2 2   d θ = M d θ

Simplificando e resolvendo para a , achamos

a = M 2 m b 1 - ( h / 2 b ) ² 2 - g

Resposta

a = M 2 m b 1 - ( h / 2 b ) ² 2 - g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

3/123) Aunidade motora A é utilizada para elevar o cilindro de 300k g a uma taxa constante de 2m / s . Se o medidor de potência B registra uma entrada de potência elétrica de 2,20k W , calcule a efici
3/134) O sistema é liberado a partir do repouso na posição mostrada . O cilindro de 15k g cai através do orifício no suporte , mas o disco de 15k g ( mostrado em corte) é removido do cilindro quando e
3/121) Um carro com uma massa de 1500k g parte do repouso na base de uma inclinação de 10 % e adquire uma velocidade de 50k m / h em uma distância de 100m com aceleração constante para cima na inclina
3/122) A resistência R à penetração x de um projétil de 0,25k g disparado com uma velocidade de 600m / s em um bloco de material fibroso é apresentada no gráfico . Represente essa resistência pela lin
3/129) O pequeno cursor de massa m é liberado a partir do repouso quando na posição A e então desliza ao longo da pista no plano vertical. A pista Elisa de A até D e rugosa .(coeficiente de atrito din