Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.12 - Ex. 132
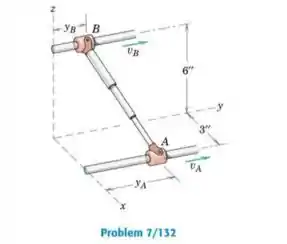
Os cursores nas extremidades da haste telescópica AB deslizam ao longo dos eixos fixos mostrados. Durante um intervalo de movimento, e . Determine a expressão vetorial para a velocidade angular da linha de centro da haste para a posição em que e .
Passo 1
Para resolvermos este problema, precisaremos encontrar a velocidade relativa entre os dois pontos e o comprimento da haste que conecta os dois pontos, como dá para perceber, eles não permanecerão paralelos o tempo todo, pois a velocidade do ponto A é maior que a velocidade do ponto B, e portanto a haste irá formar um ângulo em relação ao plano xz.
Vamos primeiro expressar a velocidade relativa:
E a distância entre os pontos será (quando ambos estiverem paralelos entre si, e não após o deslocamento dado no enunciado):
Passo 2
Para calcularmos o a velocidade angular, sabemos que precisaremos encontrar a normal do segmento AB, vamos utilizar o ângulo formado entre os pontos A e B que consideramos no Passo1 e chamá-lo de , o produto cosseno desse ângulo com a velocidade nos dará a intensidade da velocidade na direção normal ao segmento AB
Sendo que será a relação entre a situação onde A e B estão paralelos e a situação descrita no enunciado, com os valores das posições dados de cada ponto:
E a componente normal da velocidade relativa:
Passo 3
Agora podemos calcular a magnitude da velocidade angular:
Passo 4
Por fim, vamos calcular o vetor , utilizando um ângulo formado entre a coordenada x e o vetor de . Como não possui componente y, já que é perpendicular às velocidades de A e de B: