Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 7.6 - Ex. 45

Para as condições descritas no Prob. 7/36, determine a velocidade v e a aceleração a do centro A da ferramenta esférica em termos de β .

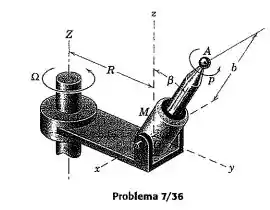
Passo 1

Para resolvermos o problema, usaremos as relações de velocidade e aceleração de um ponto dadas no livro. Também converteremos os valores para deixar no sistema SI para facilitar nossas contas.

Passo 2

Vamos começar utilizando a equação para velocidade relativa:

v A = v 0 + Ω × r A O + v r e l

Com v 0 = - R ⋅ Ω ⋅ i ^ , Ω = Ω ⋅ k ^ , r A O = b ⋅ s e n β ⋅ j ^ + b ⋅ cos ⁡ β ⋅ k ^ e v r e l = b ⋅ β ˙ ⋅ cos ⁡ β ⋅ j ^ - s e n β ⋅ k ^ . Todos dados obtidos no exercício que é usado como referência (7.36)

Agora substituindo os valores obtidos na equação inicial, temos que:

v A = - R ⋅ Ω ⋅ i ^ + Ω ⋅ k ^ × b ⋅ s e n β ⋅ j ^ + cos ⁡ β ⋅ k ^ + b ⋅ β ˙ ⋅ cos ⁡ β ⋅ j ^ - s e n β ⋅ k ^

v A = - Ω ⋅ R + b ⋅ s e n β ⋅ i ^ + b ⋅ β ˙ ⋅ ( cos ⁡ β ⋅ j ^ - s e n β ⋅ k ^ )

Para encontrarmos a aceleração, usaremos outra relação dada que se encontra derivando a relação da velocidade. Temos então que:

a A = a 0 + Ω ˙ × r A O + Ω × Ω × r A O + 2 ⋅ Ω × v r e l + a r e l

Onde:

a 0 = - R ⋅ Ω 2 ⋅ j ^ , Ω ˙ = 0 .

Ω × Ω × r A O = - Ω 2 ⋅ b ⋅ s e n β ⋅ Ω ⋅ j ^

2 ⋅ Ω × v r e l = 2 ⋅ Ω ⋅ b ⋅ β ˙ ⋅ cos ⁡ β ⋅ i ^

a r e l = b ⋅ β ˙ 2 ( s e n β ⋅ j ^ + cos ⁡ β ⋅ k ^

Assim, temos que a aceleração final será:

a A = - 2 ⋅ b ⋅ Ω ⋅ β ˙ ⋅ cos ⁡ β ⋅ i ^ - Ω 2 ⋅ R + b ⋅ s e n β + b ⋅ β ˙ 2 ⋅ s e n β ⋅ j ^ - b ⋅ β ˙ 2 ⋅ cos ⁡ β ⋅ k ^

Resposta

Resposta: v A = - Ω ⋅ R + b ⋅ s e n β ⋅ i ^ + b ⋅ β ˙ ⋅ ( cos ⁡ β ⋅ j ^ - s e n β ⋅ k ^ )

a A = - 2 ⋅ b ⋅ Ω ⋅ β ˙ ⋅ cos ⁡ β ⋅ i ^ - Ω 2 ⋅ R + b ⋅ s e n β + b ⋅ β ˙ 2 ⋅ s e n β ⋅ j ^ - b ⋅ β ˙ 2 ⋅ cos ⁡ β ⋅ k ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um cone circular reto A rola sobre o cone circular reto fixo B a uma taxa constante e executa uma volta completa em torno de B a cada quatro segundos. Calcule o módulo da aceleração angular do cone A
O pêndulo oscila em torno do eixo x de acordo com o θ =π 6 s e n 3 π t radianos, onde t é o tempo em segundos. Simultaneamente, o eixo AO gira em torno do eixo vertical z na taxa constante w z = 2 πr
99. Um carro faz uma curva para a direita em uma estrada horizontal. Determine se a reação normal sob a roda traseira direita é aumentada ou diminuída como resultado do efeito giroscópicos das rodas e
96. Um professor de dinâmica demonstra os princípios giroscópicos para seus alunos. Ele suspende uma roda que gira rapidamente com um fio preso a uma extremidade de seu eixo horizontal. Descreva o mov
97. Os dois discos idênticos estão girando livremente sobre o eixo, com velocidades angulares iguais em módulo e opostas em sentido como apresentado. O eixo por sua vez, é forçado a girar em torno do