Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 44
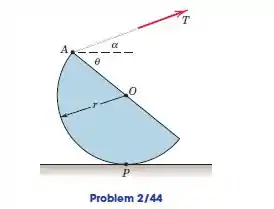
Determine o momento da tensão em relação ao ponto e ao ponto .
Passo 1
Oooi, tudo joinha?
Queremos determinar o momento da tensão em relação ao ponto e ao ponto . Vamos iniciar a resolução decompondo a tensão em e . Observe a figura:
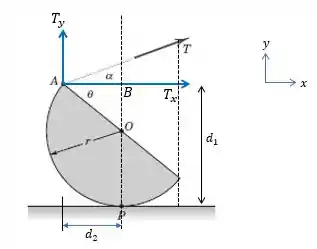
Veja que, o segmento é igual ao raio , então, olhando para o triângulo , temos:
E, também,
Agora, olhando para o segmento , notamos que,
Ou seja,
Passo 2
Vamos então, determinar o momento da tensão em relação ao ponto .
Considerando o sentido horário como positivo:
no sentido horário.
Passo 3
E, por fim, vamos encontrar o momento da tensão em relação ao ponto .
Considerando o sentido horário como positivo:
no sentido horário.
Resposta
Exercícios de Livros Relacionados
Para o anel do Problema 2.35, determine (a) o valor necessário de α para que a resultante das forças seja na vertical, (b) a correspondente intensidade da resultante.
Determine (a) a tensão de tração necessária no cabo A C , sabendo que a resultante das três forças exercida no ponto C da haste B C seja ao longo da linha B C . (b) a correspondente intensidade da res
Quatro placas são montadas numa estrutura no vão da autoestrada, e as intensidades das forças do vento horizontal exercidas nas placas são mostradas na figura. Determine a intensidade e o ponto de apl
Uma estaca é puxada do solo por meio de duas cordas como mostra a figura. Sabendo que a intensidade, direção e sentido da força exercida em uma das cordas, determine a intensidade, a direção e o senti
A direção e o sentido das forças de 330 N podem variar, mas o ângulo entre elas é sempre 50°. Determine o valor de α para que a resultante das forças atuantes em A seja na horizontal e para a esquerda