Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 22
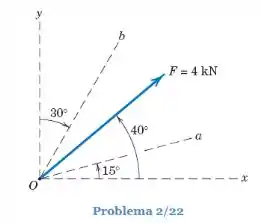
Determine os componentes e com a força de ao longo dos eixos oblíquos e . Determine as projeções de e de sobre os eixos e .
Passo 1
Oooi! Vamos lá para mais uma resolução?
Esse problema pede que determinemos as componentes e e as projeções e da força , sendo que,
Vamos determinar primeiro as componentes. Como a figura do problema nos fornece o ângulo entre o eixo a força e o ângulo entre o eixo e o eixo , montamos a figura abaixo:
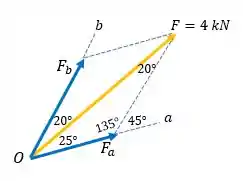
Na figura do problema, veja que,
E
Em posse desses ângulos, descobrimos os outros.
Passo 2
Agora usando a lei dos senos encontramos as componentes:
Componente :
Componente :
Passo 3
Vamos agora calcular as projeções e :
Resposta
Exercícios de Livros Relacionados
Determine a resultante das três forças do Problema 2.22.
Sabendo que a tração no cabo B C é 725N , determine a resultante das três forças exercidas no ponto B da viga A B .
Determine os componentes x e y de cada uma das forças indicadas.
O cabo A C exerce sobre a viga A B a força P dirigida ao longo da linha A C . Sabendo que P tem uma componente vertical de 1560N , determine (a) a intensidade da força P , (b) sua componente horizonta
Determine os componentes x e y de cada uma das forças indicadas.