Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 31
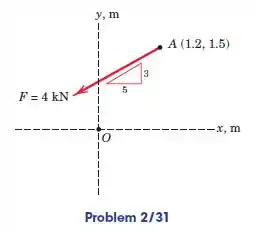
A força de é aplicada no ponto . Calcule o momento em relação ao ponto , expressando-o como um escalar e como uma quantidade vetorial. Determine os pontos nos eixos e em relação aos quais o momento de vale zero.
Passo 1
Olá, tudo joinha?
Vamos começar esse problema decompondo a força nos eixos e . Observe a figura:
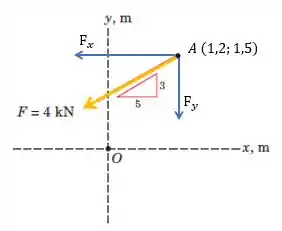
Veja que, na figura, não temos o ângulo entre a força e a componente , mas temos o triângulo retângulo, no qual,
Então, calculando o módulo das componentes, temos:
Passo 2
Calculamos o momento multiplicando a força pela distância dela até o ponto . Veja que, a força provoca um giro no sentido anti-horário, e está a uma distância de do ponto Já a força provoca um giro no sentido horário e está a do ponto .
Adotando o sentido anti-horário como positivo, temos então que,
no sentido anti-horário.
E representando como um escalar,
Passo 3
Os pontos nos eixos e em relação aos quais o momento de vale zero pertencem à linha de ação da força, ou seja, temos que achar os pontos de interseção da reta com os eixos e . Sabemos que, a equação da reta é,
Para encontrar o coeficiente , substituímos as coordenadas do ponto na equação:
Logo, a equação da reta é
Dessa forma, as interseções com os eixos e serão:
Para :
Para :
Ou seja, o momento de é nulo em relação aos pontos de coordenadas e , localizados no eixo e no eixo respectivamente.