Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 68

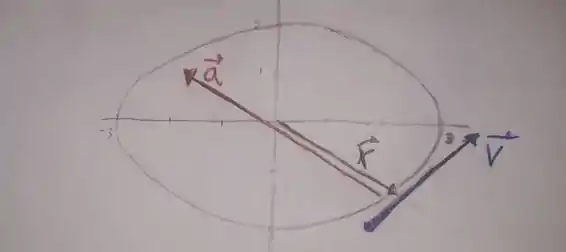
As coordenadas retangulares de uma partícula que se desloca no plano x - y são dadas por x = 3 cos ⁡ ( 4 t ) e y = 2   s e n ( 4 t ) , onde o tempo t é expresso em segundos e x e y são expressos em metros. Desenhe a posição r , a velocidade v , e a aceleração a no instante t = 1,4   s e determine os ângulos θ 1 entre v e a e θ 2 entre r e a .

Passo 1

Galera, como x e y foram dados em função de t , podemos escrever a posição r assim:

r = 3 cos ⁡ ( 4 t ) i + 2   s e n ( 4 t )   j

v = r ' = - 12   s e n 4 t i + 8 cos ⁡ ( 4 t ) j

a = v ' = - 48 cos ⁡ 4 t i - 32   s e n ( 4 t )   j

Substituindo o valor de t = 1,4   s , temos:

r = 2,327   i - 1,263   j

v = 7,575   i + 6,205   j

a = - 37,23   i + 20,20   j

Passo 2

Beleza! Agora, para calcular os ângulos θ 1 e θ 2 , será útil primeiro calcular os ângulos θ r , θ v e θ a , que cada vetor faz com o eixo x quando t = 1,4   s . Olha só:

t g   θ r = - 1,263 2,327 ≈ - 0,543

θ r = t g - 1 - 0,543 ≈ - 28,5 °

t g   θ v = 6,205 7,575 ≈ 0,819

θ v = t g - 1 0,819 ≈ 39,3 °

t g   θ a = 20,20 - 37,23 ≈ - 0,543

θ a = 180 ° + t g - 1 - 0,543 ≈ 151,5 °

Precisamos somar 180 ° no último ângulo porque a aceleração tem a coordenada x negativa e a coordenada y positiva, e não o contrário.

Passo 3

Finalmente, podemos calcular θ 1 e θ 2 :

θ 1 = θ a - θ v = 151,5 ° - 39,3 ° = 112,2 °

θ 2 = θ a - θ r = 151,5 ° - - 28,5 ° = 180 °

Show! Com todas essas informações, temos uma ideia melhor de como desenhar cada vetor:

Resposta

θ 1 = 112,2 °

θ 2 = 180 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um skatista deixa a rampa em A com uma velocidade inicial Va em ângulo 30°. Se ele atinge o solo em B, determine Va e o tempo de voo
Uma partícula move-se ao longo da trajetória circular de A para B em 1 s. Se ela leva 3 s para ir de A para C, determine a sua velocidade média quando ela vai de B para C.
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
O carro B faz uma curva de tal maneira que sua velocidade escalar é aumentada na razão de a t B = 0,5 e tm / s 2 , onde t é dado em segundos. Se um carro parte do repouso quando θ = 0 ° , determine as
Um barco está se movendo ao longo da trajetória circular com uma velocidade escalar de v = 0,0625 t 2m / s , onde t é dado em segundos. Determine a intensidade da sua aceleração quando t = 10s .