Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 81

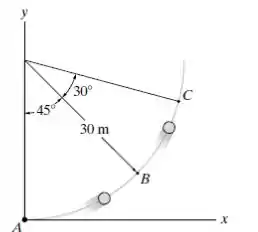
Uma partícula move-se ao longo da trajetória circular de A para B em 1 s. Se ela leva 3 s para ir de A para C, determine a sua velocidade média quando ela vai de B para C.

Passo 1

Por princípio básico temos que V = S t , assim analogamente necessitamos de um vetor posição de B para C. o qual o chamaremos de R. Este vetor funcionará como nossa variação de espaço e o tempo t, nos foi fornecido. Assim:

R B   =   R B   i   +   R B   j

R C   =   R C   i   +   R B   j

Passo 2

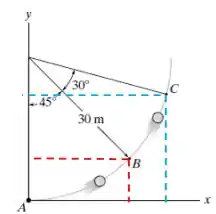
Descobriremos agora os valores de cada componente utilizando propriedades do triângulo retângulo:

Obs: do ponto A até o vértice máximo do triângulo mede-se o valor do barbante, ou seja, seu comprimento é 30 m dessa forma, portanto para encontrar as componentes verticais será 30 – (30 vezes o seno do ângulo complementar) que nos dará o valor RB j e RC j.

R B   i   =   30 s e n 45 °  

R B   j   =   30   –   30   c o s 45 °

R C   i   =   30 s e n 75 °

R C   j   =   30   –   30   c o s 75 °

Passo 3

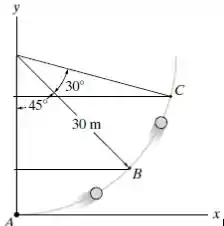
Calcularemos a velocidade para isso precisamos de um Vetor RBC que obteremos simplesmente subtraindo os vetores R C   –   R B .

R B C   =   R C   –   R B

R B C   =   ( 30 s e n 75 °   i   +   30   –   30   c o s 75 °   j   )   -   ( 30 s e n 45 °   i   +   30   –   30   c o s 45 °   j )

R B C   =   R B C   i   +   R B C   j

R B C   i   =   30 s e n 75 °   -   30 s e n 45 °   =   7,76   m

R B C   j   =   30   –   30   c o s 75 °   -   ( 30   –   30   c o s 45 ° )   =   13.45   m

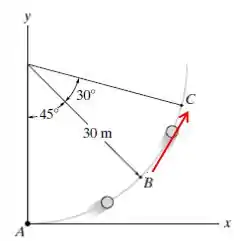
Logo:

V = ∆ S ∆ t = R B C ∆ t = 7,76   i + 13,45   j 3 - 1

Resposta

Assim a velocidade média nesse ponto será dada pelo vetor V B C   =   ( 3,88   i   +   6,72   j )   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola de golfe é batida com uma velocidade de 24m / s , como mostrado. Determine a distância d medida do lançamento até o ponto B.
Um projétil é disparado da plataforma em B. O atirador realiza o disparo da sua arma do ponto A a um ângulo de 30°. Determine a velocidade escalar da bala na boca da arma se ela atinge o projétil em C
Determine a velocidade horizontal v A de uma bola de tênis em A de maneira que ela passe raspando a rede em B. Encontre também a distância s medida a partir das redes onde a bola atinge o solo.
Um bombeiro quer direcionar o fluxo de água da sua mangueira para o fogo em B. Determine dois ângulos possíveis θ 1 e θ 2 nos quais isso pode ser feito. A água sai da mangueira a v A = 24m / s .
Um garoto em A tenta jogar uma bola sobre o telhado de um celeiro com uma velocidade escalar inicial de v A = 15m / s . Determine o ângulo θ A no qual a bola deve ser jogada de maneira que ela alcance