Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 87

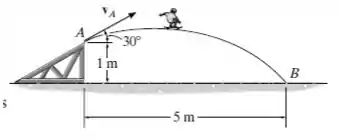
Um skatista deixa a rampa em A com uma velocidade inicial Va em ângulo 30°. Se ele atinge o solo em B, determine Va e o tempo de voo

Passo 1

Para resolver esse problema a gente vai ter que dar aquela relembrada marota de lançamento oblíquo. A coisa mais importante sobre esse tipo de lançamento é que a velocidade horizontal do nosso skatista será constante, enquanto a velocidade vertical sofrerá atuação da gravidade e, portanto, irá mudar.

Então, para o eixo x vamos utilizar as equações do movimento uniforme:

S = S 0 + v x t

Enquanto para o movimento no eixo y vamos utilizar as equações do movimento uniformemente variado:

S = S 0 + v 0 y t + a t 2 2

Passo 2

Então vamos analisar primeiro o movimento em x , para isso a gente vai ter que fazer a decomposição da velocidade na horizontal e vertical assim como

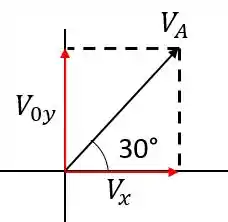
Assim, vamos obter:

V A x   =     V A   c o s 30 °

E as distâncias são

x f   = 5   m

x 0   =   0   m

Agora podemos substituir na equação da posição:

S = S o   +   V o t

Assim,

x f   =   x 0   +   ( V A x ) t

5   =   0 +   ( V A   c o s 30 ° ) t

Portanto a eq 1 é dada por:

V A = 5 t c o s 30 °

Perceba que não temos o tempo então vamos parar por aqui.

Passo 3

Isolar a equação do movimento referente ao eixo y, como mostrado no desenho anterior:

V A y   =     V A   s e n ( 30 ° )

Importante lembrar que a aceleração atuante é a da gravidade e ela é negativa porque atua para baixo:

a y =   - g = - 9,81

y f   =   0   m

obs: Estamos considerando como centro do nosso eixo cartesiano a base da rampa, logo abaixo de A.

Voltando para a nossa equação

S y = S o y   +   V o t   +   1 2 a y t ²

Tem-se,

0 = 1   +   V A s e n 30 °   t + 1 2 ( - 9,81 )   t ²  

Portanto a eq2 é dada por,

4,905 t ² -   V A s e n 30 °   t - 1 = 0

Passo 4

Agora iremos substituir uma na outra:

V A = 5 t c o s 30 °

Em:

4,905 t ² -   V A s e n 30 °   t - 1 = 0

Logo,

4,905 t ² -   5 s e n 30 ° t c o s 30 ° t - 1 = 0

4,905 t ² -   5 s e n 30 °   c o s 30 ° - 1 = 0

4,905 t ² -   5 t g ( 30 ° ) - 1 = 0

Isolando para t:

4,905 t 2 =   5 t g 30 ° + 1

t 2 =   5 t g 30 ° + 1 4,905

t = 5 t g 30 ° + 1 4,905

t   =   0,890   s

E por fim substituindo na eq 1 o valor de t,

V A = 5 0,890 × c o s 30 °

V A   =   6,49   m / s

Resposta

Assim o tempo de voo esperado é de 0,890 segundos e a velocidade que o skatista sai da rampa será de 6,49 m/s.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma bola é chutada do ponto A com a velocidade inicial v a = 10 m/s. Determine o alcance R e a velocidade escalar quando a bola tocar o solo.
Uma bola de futebol americano deve ser chutada sobre o poste do gol que fica a 4,5 m de altura. Se a sua velocidade escalar inicial é v A = 24m / s , determine se ela consegue ultrapassar o poste do g
Pacotes pequenos movendo-se sobre uma esteira transportadora caem dentro de um carrinho de carga de 1 m de comprimento. Se a esteira está se movendo com uma velocidade escalar constante de v c = 2m /
Uma bola de futebol americano é chutada sobre o poste do gol com uma velocidade de v A = 24m / s como mostrado. Determine o ponto Bx , y onde ela atinge as arquibancadas.
A velocidade do jato de água saindo do orifício pode ser obtida de v = 2 g h , onde h = 2m é a distância do orifício até a superfície livre da água. Determine o tempo para uma partícula de água deixan