Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 47
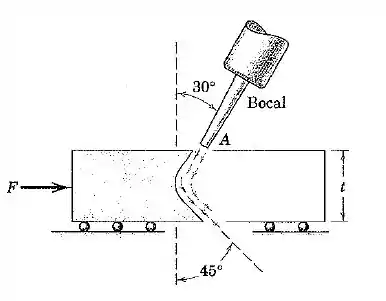
Um dos mais avançados métodos para cortar placas metálicas utiliza um jato da água em alta velocidade que carreia um pó abrasivo de granada. O jato escoa a partir do bocal de de diâmetro em e segue a trajetória indicada através da espessura da placa. Conforme a placa é lentamente deslocada para a direita, o jato executa um rasgo estreito de precisão na placa. A mistura água-abrasivo é usada à taxa baixa de e possui uma massa específica de . A água escoa da parte inferior da placa com uma velocidade que é da velocidade imposta pelo bocal. Calcule a força horizontal necessária para manter a placa contra o jato.
Passo 1
Nós podemos descobrir a força olhando para a diferenças entre as velocidades no início e no final:
Então vamos começar procurando uma expressão para essas velocidades. Começando para a velocidade da água antes de “fazer a curva”:
Onde é o volume de água que entra no sistema por unidade de tempo, e já foi dada no enunciado.
E como a velocidade “após a curva” é da velocidade inicial:
Passo 2
E agora podemos voltar à primeira equação que escrevemos:
Podemos obter a taxa de escoamento de massa a partir de :
E agora é só substituir na fórmula de cima, mas lembrando que precisamos “projetar” as forças e as velocidades na mesma direção:
Pronto!
Resposta
A força horizontal necessária é aproximadamente .