Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 5.Problemas - Ex. 80
A seção transversal de uma barragem de concreto é mostrada na figura. Para uma seção de barragem de largura de , determine (a) as forças de reação exercidas pelo solo sobre a base da barragem, (b) o ponto de aplicação da resultante das forças de pressão exercidas pela água sobre a face da barragem.
Passo 1
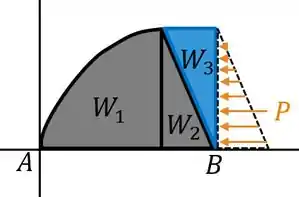
Bom galera, a gente vai começar separando o corpo sobre a viga para facilitar pra gente, vamos deixar em figuras mais simples, assim:
Passo 2
Show de bola, agora vamos calcular o peso de cada um com a seguinte fórmula:
Então vamos calcular o peso de cada parte, a primeira você vai precisar de integral para calcular a área, mas eu sei que você consegue, se precisar o responde aí tem ótimos vídeos sobre isso:
E agora vamos calcular a pressão gerada pela água que empurra no eixo horizontal:
Passo 3
Então, vamos analisar as forças na vertical e na horizontal, com a equação de equilíbrio, bem assim:
Na horizontal agora:
Passo 4
Belezinha, depois disso a gente já vai calcular o centro de massa da figura, para a gente encontrar onde a força resultante será aplicada, pra isso a gente vai montar uma tabelinha simples:
Obs.: de cada figura que a gente separou a gente consegue encontrar no final do nosso livro.
Passo 5
Por fim, vamos calcular as força de pressão que a água exerce na barragem:
E o ângulo a gente pode usar a função inversa da tangente, assim:
Resposta
(a)
(b)
(c)