Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.5 - Ex. 85
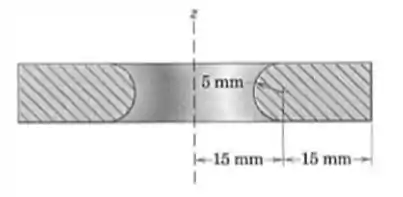
O corpo mostrado em seção transversal é uma grande arruela de Neoprene. Calcule sua área superficial A e seu volume V.
Passo 1
Vamos primeiro achar a área com base numa visão melhor da imagem abaixo, considerando somente metade (por simetria, o valor é o dobro do calculado pela imagem).
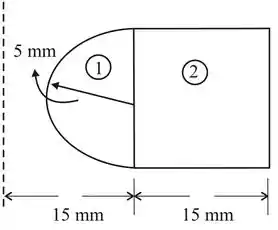
Passo 2
Logo, a nossa área é dada por:
Nosso volume é dado por:
Resposta
Exercícios de Livros Relacionados
O tanque de processamento é usado para armazenar líquidos durante a manufatura. Estime a área da superfície externa do tanque. O tanque tem topo plano e as placas com que é fabricado possuem espessur
Um anel é formado girando-se a área 360º em torno do eixo x – x . Determine sua área de superfície.
Determine a área da superfície do meio-fio. Não inclua a área das extremidades no cálculo.
Usando a integração, determine a área e a distância do centroide x da região plana sombreada. Depois, usando o segundo teorema de Pappus -Guldinus, determine o volume do sólido gerado girando-se a áre
Determine a área da superfície e o volume do anel formado girando-se o quadrado em torno do eixo vertical.