Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 94
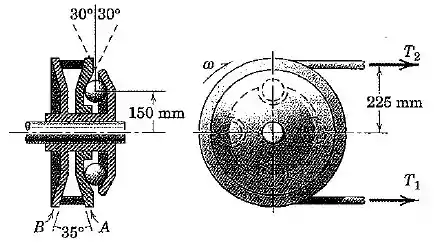
Quando uma correia em aciona uma polia em alta velocidade, a ação centrífuga tende a diminuir o seu contato com a polia e consequentemente reduzir a capacidade de transmitir torque. Um dispositivo para compensar este efeito é apresentado e consiste em um compartimento e quatro esferas que giram com a polia. As esferas são comprimidas contra as duas superfícies cônicas de e forçam o lado interno de a deslizar para a esquerda em direçao ao lado oposto , apertando assim a correia. A peça é conectada a por uma chaveta colocada na extensão do cubo da polia, de forma que esta gira com restante da polia, mas está livre para deslizar sobre . Calcule a força axial sobre provocada pela ação das esferas para uma velocidade de , se a massa de cada uma das quatro esferas é de .
Passo 1
Dê uma olhada na figura da esquerda: conforme a polia gira as esferas são “empurradas para fora” pela ação centrífuga.
Então, conforme as esferas tentam passar pela abertura pequena, elas comprimem a parede com uma certa força que mantém cada esfera em uma trajetória circular (ou seja, são forças centrípetas!):
Essa força é a componente das forças normais que aponta para o centro da polia. Como temos duas paredes pressionando cada esfera:
Passo 2
E agora chegamos na seguinte equação:
E precisamos converter a velocidade angular para :
Mas cuidado, nosso interesse é calcular a força axial sobre a parede :
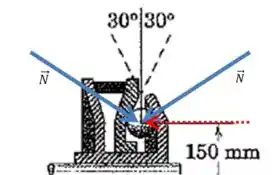
Ou seja, nosso interesse está naquela componente vermelha de uma das forças normais que agem em cada bola.
Passo 3
Então a força total que é feita sobre a parede é:
Resposta
A força sobre a parede é .