Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 99
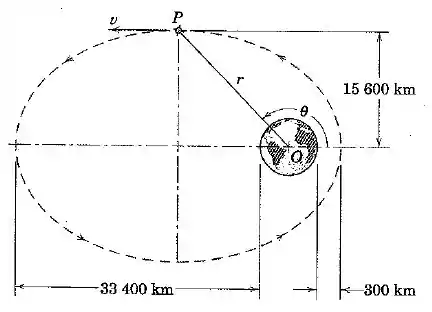
A nave espacial está na órbita elíptica mostrada. No instante representado, sua velocidade é . Determine os valores correspondentes de , , e . Utilize para a aceleração da gravidade sobre a superfície da Terra e para o raio da Terra.
Passo 1
Vamos começar dando nome a alguns ângulos na figura:
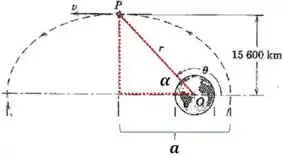
E com essa imagem já podemos encontrar uma expressão para , pois:
E a componente tangencial (que é perpendicular ao raio ) também tem uma expressão simples:
Então para determinar essas grandezas vamos precisar encontrar os valores de e de .
Passo 2
Olhando para a imagem podemos ver que pode ser determinado a partir das características da elipse:
Onde é o semi-eixo maior da elipse menos o trecho que vai do centro da Terra até a borda mais próxima da elipse!
E vamos usar a fórmula para o semi-eixo maior da elipse (lembrando que o raio da Terra é ):
E agora substituindo na equação de cima:
E agora falta calcular o raio . Olhando para a figura podemos usar o teorema de pitágoras:
E então os valores de e são:
Passo 3
Agora queremos calcular as acelerações e . Vamos analisar as forças na direção radial:
Nesse caso a única força que atua nessa direção é a gravitacional. A aceleração gerada a uma distância do centro pode ser escrita em termos da aceleração da gravidade na superfície da Terra:
E então:
Passo 4
Para calcular a aceleração na direção tangencial precisamos fazer uma coisa bem parecida com o passo :
E como não existe nenhuma força nessa direção:
Resposta
, , , .