Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.5 - Ex. 90
Para as condições indicadas no Prob. , determine as componentes inerciais e da força horizontal exercida sobre o cursor pelo tubo imediatamente antes do cursor sair do tubo.
Imgem do Prob. :
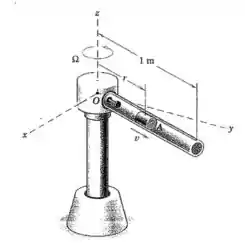
Passo 1
No problema encontramos uma fórmula para calcular a velocidade radial . Primeiro consideramos que, como não existe atrito dentro do tubo, a aceleração na direção radial é nula:
E então usamos a regra da cadeia para reescrever :
E então:
E integrando:
E então:
E vamos usar essa fórmula para calcular quanto tempo o cursor demora para deixar o tubo.
Passo 2
Vamos reescrever:
E agora vamos integrar quando vai de até , considerando que .
E agora precisamos resolver essa integral. Vamos resolver a indefinida primeiro, para deixar a resolução mais fácil de acompanhar:
E vamos chamar e para facilitar nossa vida:
E fazendo uma substituição que simplifica bastante as coisas:
E aplicando essa substituição na integral:
E a integral da secante é algo que conhecemos:
Passo 3
Agora podemos substituir o de volta para encontrar o valor de :
Com e
Ok, vamos continuar simplificando:
E agora é só lembrar que
E substituindo as constantes:
E lembrando que , e :
Passo 4
Agora lembre que precisamos calcular a integral indefinida, que é:
Ok, esse é o tempo que o cursor leva para chegar até o final do tubo, mas ainda não acabou! Vamos ver qual é o deslocamento angular:
Passo 5
Beleza, agora é só lembrar do valor que tínhamos calculado para a força no problema :
E agora fica fácil achar as componentes em e , vamos desenhar a visão de cima:
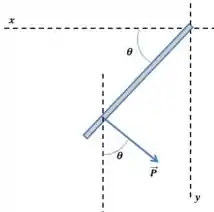
Pronto!
Resposta
As componentes da força são e .