Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 67
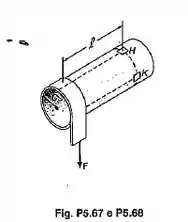
Uma correia fina é enrolada em torno de uma barra maciça de raio c, como mostrado. Sabendo-se que uma força vertical F é aplicada na correia, determinar em termos de F, c e l, as tensões, normal e de cisalhamento, no (a) ponto H; (b) ponto K.
Passo 1
Analisando a seção onde se encontram os pontos H e K
O J e I são expressos por
Passo 2
No ponto H teremos
Passo 3
Para o ponto K:
Como o ponto k está na linha neutra
Por conta do torque temos
Por conta do cisalhamento:
O total é então
Resposta
Exercícios de Livros Relacionados
Determine a variação do raio r da viga em balanço que suporta a carga distribuída uniforme, de modo que ela tenha uma tensão de flexão máxima constante σ m á x á em todo o seu comprimento.
A viga tem largura w e altura que varia como mostra a figura. Se ela suportar uma força concentrada P em sua extremidade, determine a tensão de flexão máxima absoluta na viga e especifique sua localiz
A viga tem a forma de um tronco de cone reto com diâmetro de 12 mm em A e de 300 mm em B. Se ela suportar uma força de 750 N em A, determine a tensão de flexão máxima absoluta na viga e especifique su
Selecione no apêndice B a viga de abas largas de aço que tenha o menor peso e que suportará com segurança as cargas mostradas. A tensão de flexão admissível é σ = 160M P a e a tensão de cisalhamento a
A viga afunilada simplesmente apoiada suporta a força concentrada p em seu centro. Determine a tensão de flexão máxima absoluta na viga.