Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 11.Problemas - Ex. 35

A viga tem largura w e altura que varia como mostra a figura. Se ela suportar uma força concentrada P em sua extremidade, determine a tensão de flexão máxima absoluta na viga e especifique sua localização x.

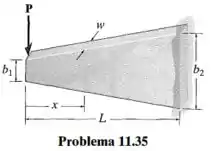
Passo 1

Para resolver a questão precisamos aplicar a equação da flexão. Porém, o momento interno e a geometria da seção mudam com a distância. Então faremos o seguinte procedimento:

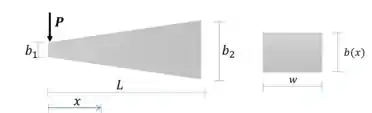
  • Encontramos uma equação para o momento fletor M ( x )
  • Encontramos uma equação para o momento de inércia I ( x )
  • Aplicamos a equação da flexão σ x = M x ⋅ c ( x ) I ( x )
  • Derivamos e igualamos a equação da flexão a zero para encontrar o ponto de máximo d σ x d x = 0
  • Utilizamos o valor encontrado para determinar a tensão máxima

Passo 2

Vamos começar calculando uma equação para o momento fletor. Note que não é preciso calcular as reações de apoio.

∑ M = 0 ⇒ P x + M x = 0

M x = - P x

Passo 3

Vamos investigar o comportamento do diâmetro ao longo da seção

O comportamento é linear, então podemos aplicar uma regressão linear:

b x - b 1 x = b 2 - b 1 L

Isolando b ( x )

b x = b 2 - b 1 L x + b 1

Passo 4

Vamos calcular as propriedades geométricas da seção:

c x = b x 2

I x = w ⋅ b x 3 12

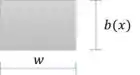
Passo 5

Vamos aplicar a equação da flexão:

σ x = M x ⋅ c x I x

σ x = P x ⋅ b x 2 w ⋅ b x 3 12

σ x = 6 P x w ⋅ b x 2

Aplicando o valor de b x

σ x = 6 P x w ⋅ b 2 - b 1 L x + b 1 2

Simplificando:

σ x = 6 P L 2 w b 2 - b 1 2 ⋅ x x + L ⋅ b 1 b 2 - b 1 2

Passo 6

Agora vamos derivar a equação para encontrar o ponto de máximo:

d σ x d x = 0

6 P L 2 w b 2 - b 1 2 ⋅ 1 ⋅ x + L ⋅ b 1 b 2 - b 1 2 - x ⋅ 2 x + L ⋅ b 1 b 2 - b 1 ⋅ [ 1 ] x + L ⋅ b 1 b 2 - b 1 4 = 0

Jogando as constantes, e o denominador pro outro lado da equação:

1 ⋅ x + L ⋅ b 1 b 2 - b 1 2 - x ⋅ 2 x + L ⋅ b 1 b 2 - b 1 ⋅ 1 = 0

Simplificando

x + L ⋅ b 1 b 2 - b 1 2 - 2 x x + L ⋅ b 1 b 2 - b 1 = 0

Pondo em evidência:

x + L ⋅ b 1 b 2 - b 1 ⋅ x + L ⋅ b 1 b 2 - b 1 - 2 x = 0

Daqui surgem duas possibilidades:

  • x + L ⋅ b 1 b 2 - b 1 = 0 ⇒ x = - L ⋅ b 1 b 2 - b 1 , valor negativo e por isso é desconsiderado
  • x + L ⋅ b 1 b 2 - b 1 - 2 x = 0 ⇒ x = L ⋅ b 1 b 2 - b 1

Assim o ponto de máximo é:

x m a x = L ⋅ b 1 b 2 - b 1

Passo 7

Basta aplicar na equação da flexão

σ m a x = 6 P L 2 w b 2 - b 1 2 ⋅ x m a x x m a x + L ⋅ b 1 b 2 - b 1 2

σ m a x = 6 P L 2 w b 2 - b 1 2 ⋅ L ⋅ b 1 b 2 - b 1 L ⋅ b 1 b 2 - b 1 + L ⋅ b 1 b 2 - b 1 2

σ m a x = 3 P 2 b 1 w ( b 2 - b 1 )

Resposta

x m a x = L ⋅ b 1 b 2 - b 1

σ m a x = 3 P 2 b 1 w ( b 2 - b 1 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas forças de 4 kN são aplicadas ao elemento de máquina AB, como mostrado. Determinar as tensões, normal e de cisalhamento, no: (a) ponto d; (b) ponto e; (c) ponto f.
O eixo mecânico de um automóvel é feito para suportar as forças e o torque mostrado. Sabendo-se que o diâmetro do eixo é de 30 mm, determinar as tensões, normal e de cisalhamento, no: (a) ponto H; (b)
A viga em balanço AB tem uma seção transversal retangular de 90 x 200 mm. Determinar: (a) o valor da força axial Q para que a tensão normal no ponto c seja -5,5 MPa; (b) as correspondentes tensões, no
A viga em balanço AB tem uma seção transversal retangular de 90 x 200 mm. Sabendo-se que a intensidade da força axial Q é 35,5 kN, determinar as tensões, normal e de cisalhamento, nos três pontos indi
Várias forças são aplicadas ao tubo mostrado. Sabendo-se que o tubo tem diâmetro, interno e externo, de 40 mm e de 48 mm, respectivamente, determinar as tensões normal e de cisalhamento no: (a) ponto