Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 112
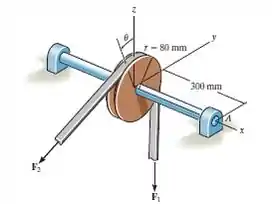
A correia passando pela polia está sujeita a duas forças e , cada uma tendo uma intensidade de . atua na direção . Substitua essas forças por uma força e um momento de binário equivalentes no ponto . Expresse o resultado em forma de vetor cartesiano. Considere .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
A ideia aqui é substituir as duas forças dadas no enunciado da questão por uma força resultante e por um momento , ambos em relação ao ponto .
Em relação a força resultante, precisamos escrever a força na forma vetorial primeiramente. Depois, basta fazermos a soma, coordenada a coordenada, para obtermos a força resultante.
Já em relação ao momento, vamos ter que calcular o momento devido a todas as forças em relação ao ponto . Para isto, posteriormente, iremos utilizar a notação vetorial para facilitar as contas!
Então, vamos aos cálculos!
Passo 2
Primeiramente, vamos determinar a força resultante.
Nosso primeiro passo é escrever a força na forma vetorial. Para isto, precisamos decompor ela utilizando trigonometria (escrever as componentes na direção e ). Sendo assim, temos:
Como a força , a força resultante é:
E assim finalizamos a primeira parte da questão!
Passo 3
Para finalizarmos, temos que calcular o momento em relação ao ponto . Para facilitar a nossa vida, como as forças estão inclinadas, em relação aos eixos coordenados, vamos trabalhar aqui com a forma vetorial.
Portanto, vamos calcular os momentos vetorialmente e depois fazer a soma deles. Começando pela força , temos:
Lembrem-se que o vetor é o vetor distância da origem até o ponto de aplicação da força .
Já para a força , temos:
Portanto, o momento resultante é:
E assim finalizamos a questão!
Resposta
A força resultante é
E o momento de binário é