Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 142

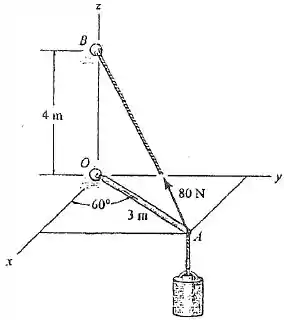
142. O cabo A B exerce uma força de 80   N sobre a extremidade da barra de 3   m de comprimento O A . Determine a intensidade da projeção dessa força ao longo da barra.

Passo 1

Primeiro para resolver essa questão temos que achar o vetor unitário que tenha a mesma direção que a força de 80   N para podermos escrever a força de forma vetorial, para isso vamos usar a fórmula:

F → = F ⋅ u →

Onde F = 80   N .

Sendo u → o vetor unitário com a mesma direção de F .

Depois que acharmos a força expressa em forma vetorial basta multiplicá-la pelo vetor unitário na direção de O A , obtendo assim a intensidade da força ao longo de O A .

Passo 2

O vetor unitário que tem a mesma direção que o eixo A B , é dado por:

u → = r A → r A →

Onde r A → é o vetor que sai do ponto A até o ponto B .

Assim:

r A → = { - 3 ⋅ cos ⁡ 60 ° i - 3 ⋅ s e n   60 ° j + 4 k }

= { - 3 ⋅ 0,5 i - 3 ⋅ 0,866 j + 4 k }

r A → = - 1 , 5 2 + - 2 , 59 2 + 4 2

= 2,25 + 6 , 7 1 + 1 6

24,96 = 4,99

Logo:

u → = { - 1 , 5 i - 2 , 59 j + 4 k } 4,99

= { - 0,3 i - 0 , 52 j + 0 , 8 k }

Logo F → pode ser obtida com a seguinte operação:

F → = F ⋅ u →

= 8 0 ⋅ - 0 , 3 i - 0 , 52 j + 0 , 8 k

⇒ F → = ( - 24 i - 41,6 j + 64 k )

Passo 3

Agora precisamos achar o vetor unitário na direção de O A , vamos usar o mesmo raciocínio que para o F .

O vetor unitário que tem a mesma direção que o eixo O A , é dado por:

v → = r O → r O →

Onde r O → é o vetor que sai do ponto O até o ponto A . Assim:

r O → = { 3 ⋅ cos ⁡ 60 ° i + 3 ⋅ s e n   60 ° j + 0 k }

= { 3 ⋅ 0,5 i + 3 ⋅ 0,866 j + 0 k }

r O → = 1,5 2 + 2,59 2 + 0 2

= 2,25 + 6,71

8,96 = 2 , 99

Logo:

v → = { 1 , 5 i + 2 , 59 j + 0 k } 2 , 99

= { 0 , 50 i + 0 , 86 j + 0 k }

Passo 4

Agora só temos que multiplicar F → por v → , então:

F → ⋅   v → = { - 24 i - 41,6 j + 64 k } ⋅ { 0,50 i + 0,86 j + 0 k }

= - 2 4 ⋅ 0 , 5 - 41,6 ⋅ 0 , 86 + 64 ⋅ 0

= - 12 - 35,77 + 0 = - 47,77

Logo a intensidade é 47,77   N , encontramos o resultado com sinal negativo pois indica que a força tem sentido contrário ao vetor unitário.

Resposta

A intensidade da componente projetada da força ao longo de O A é:

47   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua o sistema de forças e momentos binário que agem sobre o bloco retangular por um torsor. Especifique a intensidade da força e o momento de binário do torsor e a posição onde sua linha de ação
Se F a = 7 k NeF b = 5 k N , substitua o sistema de forças que age sobre as mísulas por uma força resultante e especifique sua posição sobre o plano x - y .
Determine as intensidades de F aeF b de modo que a força resultante passe pelo ponto O da coluna.
Substitua as três forças atuando na chapa por um torsor. Especifique a intensidade da força e o momento de binário para o torsor e o ponto P ( x , y ) onde sua linha de ação intercepta a chapa.
Se F a = 40 k N e F b = 35 k N , determine a intensidade da força resultante e especifique a posição de seu ponto de aplicação ( x , y ) sobre a placa.