Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 4.Problemas - Ex. 115

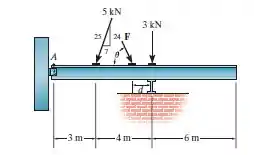
Determine a intensidade e a direção θ da força F e sua posição d na viga de modo que o sistema de carregamento seja equivalente a uma força resultante de 12   k N agindo verticalmente para baixo no ponto A e um momento de binário em sentido horário de 50   k N ⋅ m .

Passo 1

E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!

A questão nos pede para substituirmos as três forças do desenho por uma única força vertical para baixo igual a 12   k N e um momento de binário no sentido horário igual a 50   k N ⋅ m .

Mas, para fazermos esta substituição, temos que determinar quem é a força F , a direção θ e a distância d .

Portanto, temos que trabalhar com duas frentes. Primeiro vamos trabalhar com o somatório das forças. Lembrando, a força resultante é:

F R = ∑ F

Para nos auxiliar nesta etapa, vamos trabalhar com a notação vetorial, sendo a direção y vertical e positiva para cima, e x horizontal positiva para a direita.

Depois, para descobrirmos a distância d , vamos trabalhar com o somatório dos momentos. Portanto,

M R A = ∑ M A

Então, vamos aos cálculos!

Passo 2

Primeiramente, vamos trabalhar com a relação da força resultante. Sabemos que ela é vertical para baixo. Portanto,

F R = F R y j →

F R = - 12 j →   k N

Mas como a força resultante é obtida pelo somatório das outras forças, temos:

F R = ∑ F

- 12 j → = 5 ⋅ - 7 25 i → - 24 25 j → + F ⋅ cos ⁡ θ i → - sen ⁡ θ j → - 3

- 12 j → = - 7 5 + F ⋅ cos ⁡ θ i → + - 24 5 - F ⋅ sen ⁡ θ - 3 j →

Comparando coordenada a coordenada, temos o seguinte sistema:

- 7 5 + F ⋅ cos ⁡ θ = 0 - 24 5 - F ⋅ sen ⁡ θ - 3 = - 12

Cuja resposta é F = 4,42   k N e θ = 71,6 °

E assim finalizamos a primeira parte da questão!

Passo 3

Agora temos que descobrir a distância d finalizarmos. Antes de começarmos a calcular os momentos, é importante lembrarmos que as componentes horizontais das forças não causam momentos!!!

Sabemos disso pois a componente horizontal, na direção x , é colinear com o ponto A ! Portanto, vamos considerar apenas as componentes y e o momento de binário já existente na questão!!!

Tomados os devidos cuidados, vamos para os cálculos! Fazendo o somatório dos momentos, temos:

M R A = ∑ M A

F R y ⋅ 0 - 50 = - 5 ⋅ 24 25 ⋅ 3 - F ⋅ sen ⁡ θ ⋅ 7 - d - 3 ⋅ 7

- 50 = - 72 5 - 4,42 ⋅ sen ⁡ 71,6 ° ⋅ 7 - d - 21

7 - d = - 73 5 4,42 ⋅ sen ⁡ 71,6 °

7 - d = 3,48

d = 3,52   m

OBS: Lembrando, o momento é positivo quando rotaciona no sentido anti-horário! Além disto, a força resultante está aplicada no ponto A . Sendo assim, o momento devido a esta força é nulo!

E assim finalizamos a questão!

Resposta

A força F possui intensidade de 4,42   k N e uma direção θ = 71,6 ° . Já a distância d é 3,52   m .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro A B medida a partir de A .
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro medida a partir de A .
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta a viga medida a partir de O .
Substitua o carregamento do sistema por uma força resultante equivalente e especifique onde a linha de ação da resultante intercepta o membro medida a partir de A .
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto A .