Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 204

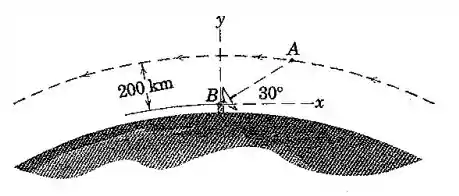
Uma estação de radar B situada no equador observa um satélite A em uma órbita circular equatorial de 200 km de altitude e se movendo de oeste para leste. Para o instante em que o satélite está 30 ° acima do horizonte, determine a diferença entre a velocidade do satélite em relação à estação de radar, quando medida a partir de um sistema de referencia sem rotação, e a velocidade quando medida em relação ao sistema de referencia do sistema de radar.

Passo 1

Bom pessoal, vamos buscar no apêndice D/2 as informações necessárias para a resolução do problema.

R = 6378   k m

ω = 7,292 × 10 - 5 r a d / s

Agora, vamos fazer um esboço da questão.

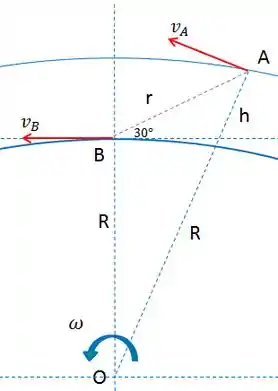
Podemos encontrar a distancia r aplicando a lei dos cossenos no triângulo ABO:

R + h 2 = R 2 + r 2 - 2 R r c o s 120 °

6378 + 200 2 = 6378 2 + r 2 - 2 6378 r c o s 120 °

r 2 + 6378 r - 2591200 = 0

Resolvendo esta equação de segundo grau, e pegando a raiz positiva, pois r é uma medida de distância, temos:

r = 383,2 k m

Passo 2

A velocidade para A em relação a B medida por uma referencia sem rotação, neste caso, o centro O pode ser escrita como a diferença entre as duas velocidades.

v = v A - v B

Já a velocidade de A medida pela referência B é v r e l e pode ser escrita pela equação:

v A = v B + ω × r + v r e l

Relacionando as duas equações acima:

v A - v B - v r e l = ω × r

∆ v = 7,292 × 10 - 5 k ^ × 383 2 00 ( c o s 30   i ^ + s e n 30 j ^ )

∆ v = 24,19930   j ^ - 13,97147 i ^ m s       ( × 3,6   k m / h )

∆ v = - 50,3 i ^ + 87,1 j ^ k m h

Resposta

∆ v = - 50,3 i ^ + 87,1 j ^ k m h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O mecanismo do Prob.5/75 é reapresentado aqui. Cada uma das barras deslizantes A e B se acopla sem deslizar na sua respectiva borda das duas rodas rebitadas. Se, além da informação apresentada, a barr
No instante representado, θ = 45 ° e a placa triangular ABC possui uma velocidade angular no sentido anti-horário de 20 rad/s e uma aceleração angular no sentido horário de 100 rad/s². Determine os mó
O movimento plano da placa triangular ABC é controlado pela manivela AO e pela barra DB. Para o instante representado, quando AO e DB são verticais, AO possui uma velocidade angular no sentido horário
A placa triangular, reapresentada aqui a partir do Prob. 5/76, possui uma velocidade angular no sentido horário de 3 rad/s e AO possui aceleração angular nula para o instante representado. Determine a
O mecanismo do Prob. 5/88 é apresentado novamente aqui. Se AO possui uma velocidade angular constante no sentido anti-horário ω O = 10r a d / s , calcule a aceleração angular da barra AB para a posiçã