Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.8 - Ex. 205

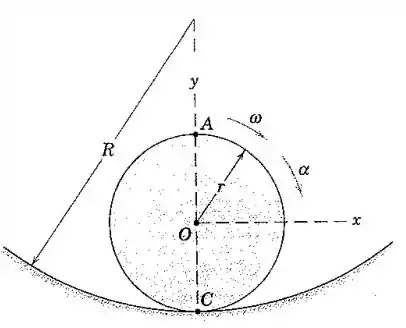
A roda rola sobre a superfície circular sem deslizar. Na posição mais baixa, possui uma velocidade angular ω e uma aceleração angular α , ambas no sentido horário. Para essa posição, obtenha expressões para a aceleração do ponto C na roda em contato com a trajetória e para a aceleração do ponto A.

Passo 1

Bom pessoal, a figura da questão está representada aqui embaixo.

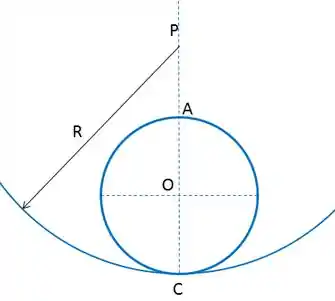
A partir da velocidade angular da roda, e sabendo que C é o centro instantâneo de velocidade nula (pois não há deslizamento), nós podemos calcular a velocidade absoluta do centro O:

v O = - ω k ^ × r j ^ = ω r   i ^   m / s

A aceleração do centro O pode ser escrita pelas suas componentes normal e tangencial em relação ao centro da trajetória de raio R:

a O = a O n + a O t

Onde:

a O t = - α k ^ × r j ^ = α r   i ^   m / s 2

a O n = ω × ω × r O P = - r O P ω 2 = - v O 2 r O P = - r ω 2 R - r - j ^ = r ω 2 R - r j ^

Então:

a O = α r   i ^ + r ω 2 R - r j ^   m / s 2

Para achar a aceleração de C, podemos usar a equação da aceleração relativa entre C e O:

a C = a O + a C / O n + a C / O t

Onde

a C / O n = ω × ω × r = - r ω 2 - j = r ω 2 j ^   m / s 2

a C / O t = α × r = - α k ^ × - r j ^ = - α r   i ^   m / s 2

Substituindo os valores na equação:

a C = α r   i ^ + r ω 2 R - r j ^ + r ω 2 j ^ - α r   i ^

a C = ω 2 r 2 R - r + r = ω 2 r 2 + R r - r 2 R - r

a C = r ω 2 1 - r R   j ^

Passo 2

Para a aceleração do ponto A, vamos fazer a mesma coisa do passo anterior, relacionando com o centro da roda O.

a A = a O + a A / O n + a A / O t

Onde

a A / O n = ω × ω × r = - r ω 2 j = - r ω 2 j ^   m / s 2

a A / O t = α × r = - α k ^ × r j ^ = α r   i ^   m / s 2

Substituindo os valores na equação:

a A = α r   i ^ + r ω 2 R - r j ^ - r ω 2 j ^ + α r   i ^

a A = 2 α r   i ^ + ω 2 r 2 R - r - r j ^ = 2 α r   i ^ + ω 2 r 2 - R r + r 2 R - r j ^

a A = 2 α r   i ^ + r ω 2 2 r R - 1 1 - r R j ^

Resposta

a C = r ω 2 1 - r R   j ^

a A = 2 α r   i ^ + r ω 2 2 r R - 1 1 - r R j ^

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A manivela giratória ED e o elemento de ligação CD obrigam a estrutura rígida ABO a oscilar em torno de O. Para o instante representado, ED e CD são ambos perpendiculares a FO, e a manivela ED possui
O mecanismo de implantação para a lança do magnetometro da nave espacial do Prob. 5/87 é novamente apresentado aqui. O elemento de acionamento OB possui uma velocidade angular constante no sentido hor
Os componentes de uma serra mecânica alternativa são apresentados na figura. A lamina de serra é montada em um arco que desliza ao longo da guia horizontal. Se o motor fira o volante a uma velocidade
Se a haste do pistão do cilindro hidráulico C tem uma velocidade constante para cima de 0,5 /s, calcule a aceleração do ponto D para a posição que θ é igual a 45 ° .
Por um curto intervalo de movimento, a barra AO possui uma velocidade angular constante ω = 4 r a d / s . Determine a aceleração angular α A B da barra AB para o instante em que AO esta paralela ao ei