Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas fundamentais - Ex. 3
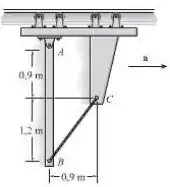
A barra de está presa com pino a uma estrutura em movimento em e é mantida em uma posição vertical por uma corda que ode suportar uma tração máxima de sem romper a corda. Quais são as componentes correspondentes à reação no pino ?
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
O exercício nos pede as componentes correspondentes à reação no pino
Para determinar a aceleração do sistema, podemos analisar o momento provocado pela aceleração:
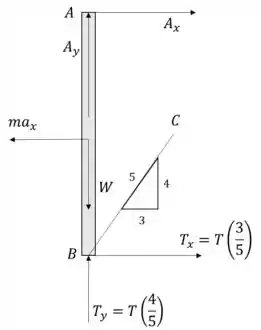
OBS: Vamos usar o valor da massa , pois foi dito no enunciado que este era o valor aproximado.
Passo 2
Agora vamos à análise horizontal:
Para a análise dinâmica das forças verticais, temos:
Sabemos que a aceleração do sistema no eixo é nula, portanto:
Resposta
Exercícios de Livros Relacionados
Se a barra AB do mecanismo de quatro barras possui uma velocidade angular constante no sentido anti-horário de 40 rad/s durante um intervalo que inclui o instante representado, determine a aceleração
O mecanismo do prob 5/118 é reapresentado aqui, onde a tira flexível F presa ao setor E recebe uma velocidade constante de 4 m/s conforme mostrado. Para o instante em que BD este perpendicular a AO, d
No projeto desse mecanismo, o movimento da placa quadrada é controlado pelas duas barras articuladas. A barra AO possui uma velocidade angular constante ω = 4 r a d / s durante um curto intervalo de m
16.97. A unidade de bombeamento de petróleo consiste de um balancim A B , a barra de conexão B C e a manivela C D . Se a manivela gira com uma taxa constante de 6 r a d / s , determine a velocidade da
Os componentes do dispositivo de comutação do prob. 5/85 são mostrados novamente aqui. Se a velocidade v da haste de controle é de 0,9 m/s e está diminuindo na taxa de 6 m/s² quando θ = 60 ° , determi