Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 16.Problemas - Ex. 152

No instante mostrado, o carro B se desloca com uma velocidade de 15 m/s, que está aumentando a uma taxa constante de 2 m/s², enquanto o carro C se desloca com uma velocidade de 15 m/s, que está aumentando a uma taxa constante de 3 m/s². Determine a velocidade e a aceleração do carro A em relação ao carro C.

Passo 1

Começaremos o exercício esquematizando o eixo de referência para rotação xyz, que estará sob o carro C conforme esquematizado na figura a seguir:

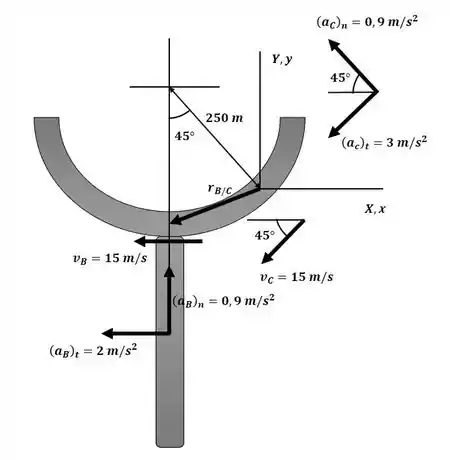
Uma vez que os carros B e C se movem numa trajetória circular, suas componentes normais da aceleração podem ser dada por:

a B n = v B 2 ρ = 15 2 250 → a B n = 0,9   m / s 2

a C n = v C 2 ρ = 15 2 250 → a C n = 0,9   m / s 2

Sendo assim, o movimento dos carros B e C com relação ao eixo de referência XYZ é:

v → B = - 15 i →   m / s

a → B = 2 i → + 0,9 j →   m / s 2

v → C = - 15 c o s 45 ° i → - 15 s e n 45 ° j → = - 10,607 i → - 10,607 j →   m / s

a → C = 0,9 c o s 45 ° - 3 c o s 45 ° i → + 0,9 s e n 45 ° - 3 s e n 45 ° j →

a → C = - 2,758 i → - 1,485 j →   m / s 2

Sua velocidade e aceleração angular pode ser dada por:

ω = v C ρ = 15 250 → ω = 0,06   r a d / s = - 0,06 k →   r a d / s

ω ˙ = a C t ρ = 3 250 → ω ˙ = 0,012   r a d / s 2 = - 0,012 k →   r a d / s 2

Passo 2

E da figura apresentada no passo 1:

r → B / C = - 250 s e n 45 ° i → - 250 - 250 c o s 45 ° j → = - 176,78 i → - 73,22 j →   m

Agora iremos aplicar a equação da velocidade relativa para os pontos B e C:

v → B = v → C + ω × r → B / C + v → r e l x y z

- 15 i → = - 10,607 i → - 10,607 j → + - 0,06 k → × - 176,78 i → - 73,22 j → + v → r e l x y z

- 15 i → = - 15 i → + v → r e l x y z

v → r e l x y z = 0   m / s

Passo 3

Agora iremos aplicar a equação da aceleração relativa para os pontos B e C com base no diagrama do passo 1:

a → B = a → C + ω ˙ B C × r → B / C + ω B C × ω B C × r → B / C + 2 ω B C × v r e l x y z + a r e l x y z

- 2 i → + 0,9 j → = - 2,758 i → - 1,485 j → + - 0,012 k → × - 176,78 i → - 73,22 j → + - 0,06 k → × - 0,06 k → × - 176,78 i → - 73,22 j → + 2 - 0,06 k → × 0 + a → r e l x y z

- 2 i → + 0,9 j → = - 3 i → + 0,9 j → + a → r e l x y z

a → r e l x y z = 1 i →   m / s 2

Resposta

v → r e l x y z = 0   m / s

a → r e l x y z = 1 i →   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A configuração mostrada é projetada para produzir a oscilação do recipiente de pequenas peças em torno de C, como parte de um processo de produção. Obtenha uma expressão para a aceleração angular α do
A carga P é abaixada pelas duas polias que estão presas uma a outra e giram como um só conjunto. Para o instante representado, o tambor A possui uma velocidade angular no sentido anti-horário de 4 rad
Calcule a aceleração angular da placa na posição mostrada, onde a barra de controle AO possui uma velocidade angular constante ω O A = 4 r a d s eθ = 60 ° para ambas as barras.
A barra AB do Prob. 5/72 é reapresentada aqui. Se a velocidade do ponto A é de 3 m/s para a direita e é constante para um intervalo incluindo a posição mostrada, determine a aceleração tangencial do p
A barra AO possui uma velocidade angular constanteω no sentido anti-horário durante um curto intervalo de seu movimento. Para a posição mostrada determine as acelerações angulares de AB e BC.