Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 119

Uma corrente é suspensa entre pontos na mesma altura e espaçados a uma distância de 20   m . Se tiver um peso por unidade de comprimento de 10   N / m e a flecha for 1   m , determine a tração máxima na corrente.

Passo 1

Que tal desenharmos a situação, para entendermos um pouco melhor o que está rolando?

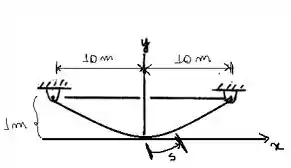
Por motivos de simetria, a origem das coordenadas é localizada no centro do cabo. A curva de deflexão é expressa como y = f ( x ) . Podemos determiná-la primeiro aplicando a seguinte equação:

x = ∫ d s 1 + 1 F H 2 ∫ w o   d s 2 1 2

Integrando, temos:

x = F H w o s e n h - 1 1 F H w o s + C 1 + C 2

x = F H 10 s e n h - 1 1 F H 10 s + C 1 + C 2

Além disso, temos também que:

d y d x = 1 F H ∫ w o d s

d y d x = 1 F H ( 10 s + C 1 )

Quando s = 0 , temos que d y d x = 0 . Isso acaba por implicar que C 1 é também igual a zero!

Passo 2

Para avaliar as constantes, vamos analisar as condições de contorno do problema. Quando x = 0 , s = 0 na equação para x , encontrada no passo 1. Usando o resultado C 1 = 0 , implica em C 2 = 0 e assim:

s = F H w o s e n h w o F H x

Substituindo na expressão na expressão de d y / d x , temos:

d y d x = s e n h w o F H x

Aplicando a integral, temos:

y = F H w o cosh ⁡ w o F H x + C 3

Se a condição de contorno y = 0 em x = 0 for aplicada, a constante C 3 = - F H / w o e, portanto, a curva de deflexão se torna:

y = F H w o cosh ⁡ w o F H x - 1

Passo 3

Em x = 10   m e y = 1   m , temos:

1 = F H 10 cosh ⁡ 10 0 F H - 1

10 F H = cosh ⁡ 10 0 F H - 1

Pelo método de tentativa e erro, encontramos que F H = 501,67   N

Passo 4

Quando x = 10   m , nós temos o valor máximo para o ângulo ( θ = θ m a x ). Assim,

t a n θ m a x = ⅆ y ⅆ x x = 10 = s e n h 10 10 501,67

θ m a x = 11,34 6 °

Logo, a tração máxima é dada por:

T m a x = F H c o s θ m a x

T m a x = 501,67 cos ⁡ 11,346 °

T m a x = 511,8   N

Resposta

A tração máxima é igual a:

T m a x = 511,8   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

132- A força cortante, em quilonewtons, em uma determinada viga é dada por V = 33 x - 7 x 3 , onde x é a distância, em metros, medida ao longo da viga. Determine, em quilonewtons por metro de comprime
128- Desenhe os diagramas de cortante e de momento para a viga mostrada. Determine a distância b, medida a partir da extremidade esquerda, ao ponto entre os suportes onde o momento fletor é nulo.
139- A carga distribuída decresce linearmente de 4 para 2 kN/m, em uma distância de 2 m ao longo de uma certa viga em equilíbrio. Se o cortante e o momento fletor na seção A valem +3kN e +2 kN.m respe
133- Sabe-se que resistência a flexão de uma viga com largura uniforme é proporcional ao quadrado da espessura y da viga. Para a viga em balanço mostrada. A espessura vale h , no apoio. Determine em f
136- Construa os diagramas de cortante e de momento para a viga carregada pelas cargas pontual e distribuída. Quais são os valores do cortante e do momento em x = 6 ? Determine o momento fletor máximo