Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 135
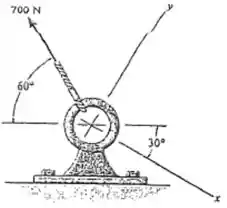
135. Determine as componentes e da força de
Passo 1
Para resolver essa questão vamos pensar um pouquinho, se os eixos e estivessem em suas posições “tradicionais” é possível ver que a força faria um ângulo de com o eixo e com o eixo .
Mas realizando uma rotação de da forma como é mostrado na figura temos uma nova situação:
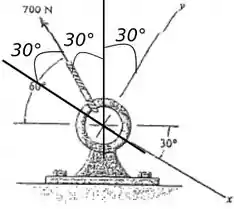
Com isso nossa força faz um ângulo de com o eixo e um ângulo de com eixo .
Passo 2
Agora para achar as componentes da força basta a fazer o seguinte:
Vamos calcular as forças:
Resposta
Exercícios de Livros Relacionados
Um cabo esticado entre o suporte fixo AeB está sob uma tensão trativa de 2k N . Expresse a tensão como um vetor usando, os vetores unitários iej , primeiro, e como uma força T A atuando em A e como um
As três forças atuam perpendiculares à placa retangular, como mostrado. Determine os momentos M 1d eF 1 ,M 2d eF 2eM 3d eF 3 , todos em relação ao ponto O .
Substitua as três forças mostradas por um sistema força-binário equivalente no pontoA . Determine a distância d abaixo do ponto A em sua linha de ação, se as forças forem substituídas por uma força re
Quatro forças atuam no olhal, como mostrado. Se o efeito resultante delas sobre o parafuso é um esforço trativo de 3k N na direção x , determine os valores necessários de θeT .
O braço A B gira na faixa 0≤θ≤180 ° e a mola não está esticada quando θ=90 ° . Determine, em função de θ , o momento em torno de O causado pela força aplicada pela mola em B . Faça um gráfico das três